
分析 (1)根据函数的单调性求出m的范围,从而求出m的值;
(2)根据函数的奇偶性得到f(a+1)<f(4-3a),根据函数在R上递增,得到a+1<4-3a,求出a的范围即可.
解答 解 (1)∵函数在(0,+∞)上递增,
∴9-3m>0,解得m<3,…(2分)
又m∈N*,
∴m=1,2.…(3分)
又函数图象关于原点对称,
∴3m-9为奇数,故m=2.…(5分)
∴f(x)=x3…(6分)
(2)∵f(a+1)+f(3a-4)<0,
∴f(a+1)<-f(3a-4)…(7分)
又f(x)为奇函数,
∴f(a+1)<f(4-3a)…(9分)
又函数在R上递增,
∴a+1<4-3a…(11分)
∴$a<\frac{3}{4}$.…(12分)
点评 本题考查了幂函数的性质,考查函数的单调性、奇偶性问题,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
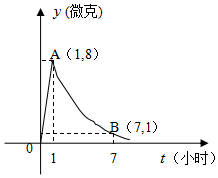 某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.
某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
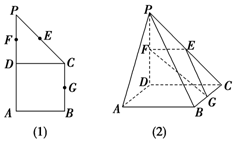 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
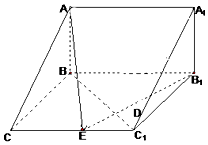 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com