已知实数a,b满足a+b=1,则(a+2)2+(b+2)2的最小值为________.

分析:由题意(a+2)
2+(b+2)
2的几何意义是点(a,b)与点(-2,-2)的距离的平方,(a+2)
2+(b+2)
2的最小值点(-2,-2)到直线a+b=1的距离的平方,由此问题转化为求点(-2,-2)到直线a+b=1的距离
解答:由题意(a+2)
2+(b+2)
2的几何意义是点(a,b)与点(-2,-2)的距离的平方
实数a,b满足a+b=1,即点(a,b)在直线a+b=1运动,
∴两点(a,b)与点(-2,-2)的距离的最小值即为点(-2,-2)到直线a+b=1的距离
由于d=
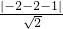
=
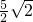
∴(a+2)
2+(b+2)
2的最小值为

故答案为:

.
点评:本题考查圆的方程的应用,点到直线的距离公式,解题的关键是理解题意,将求(a+2)
2+(b+2)
2的最小值问题转化为点(-2,-2)到直线a+b=1的距离的平方,本题考查了转化的思想,数形结合的思想,本题考查析几何的根本问题,题目难度不大,但很有价值.


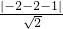 =
=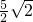

 .
.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案