
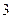 名男生和
名男生和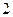 名女生中任选
名女生中任选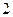 人去参加培训,用
人去参加培训,用 表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件
表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件 的对立事件,并求事件
的对立事件,并求事件 的概率;
的概率;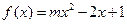 ,那么任意
,那么任意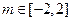 ,使函数
,使函数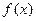 在实数集上有零根的概率.
在实数集上有零根的概率. 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:不详 题型:解答题

| 组号 | 分组 | 频数 | 频率 |
| 第1组 | 【160.165】 | 5 | 0.050 |
| 第2组 | 【165.170】 | ① | 0.350 |
| 第3组 | 【170.175】 | 30 | ② |
| 第4组 | 【175.180】 | 20 | 0.200 |
| 第5组 | 【180.185】 | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
 4、5组中用分层抽样法抽取6名学生进入第二轮面试,问第3、4、5组每组各抽取多少名学生进入第二轮面试?
4、5组中用分层抽样法抽取6名学生进入第二轮面试,问第3、4、5组每组各抽取多少名学生进入第二轮面试?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.频率是随机的,在试验前不能确定,随着试验次数的增加,频率越来越接近概率 |
B.若随机事件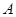 发生的概率为 发生的概率为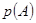 ,则 ,则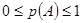 |
| C.互斥事件不一定是对立事件,但是对立事件一定是互斥事件 |
| D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性相同 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
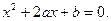 (1)若
(1)若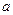 是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若
是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若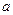 是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
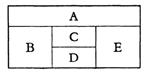
 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率; 求
求 的分布列和数
的分布列和数 学期望E
学期望E
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.5 | B.0.6 | C.0.7 | D.0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com