
【题目】已知抛物线![]() 焦点为
焦点为![]() ,且
,且![]() ,
,![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() 为坐标原点,
为坐标原点,![]() 为定值,当
为定值,当![]() 变化时,始终有
变化时,始终有![]() ,求定值
,求定值![]() 的大小;
的大小;
(3)若![]() ,
,![]() ,
,![]() ,当
,当![]() 改变时,求三角形
改变时,求三角形![]() 的面积的最大值.
的面积的最大值.
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线上一定点
,抛物线上一定点![]() .
.
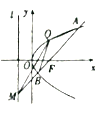
(1)求抛物线![]() 的方程及准线
的方程及准线![]() 的方程;
的方程;
(2)过焦点![]() 的直线(不经过
的直线(不经过![]() 点)与抛物线交于
点)与抛物线交于![]() 两点,与准线
两点,与准线![]() 交于点
交于点![]() ,记
,记![]() 的斜率分别为
的斜率分别为![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:

下面是![]() 关于
关于![]() 的折线图:
的折线图:
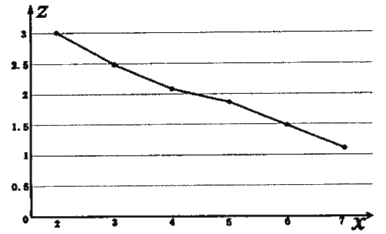
(1)由折线图可以看出,可以用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的回归方程并预测某辆
的回归方程并预测某辆![]() 型号二手汽车当使用年数为9年时售价大约为多少?(
型号二手汽车当使用年数为9年时售价大约为多少?(![]() 、
、![]() 小数点后保留两位有效数字).
小数点后保留两位有效数字).
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
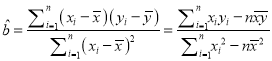 ,
,![]() .
. 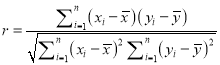 .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,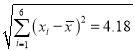 ,
,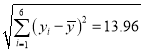 ,
,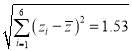 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……,依等差数列逐年递增.
(Ⅰ)设使用n年该车的总费用(包括购车费用)为f(n),试写出f(n)的表达式;
(Ⅱ)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,分别记录了4月1日至4月5日每天的昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 12 | 11 | 13 | 10 | 8 |
发芽率 | 26 | 25 | 30 | 23 | 16 |
(1)从这5天中任选2天,求至少有一天种子发芽数超过25颗的概率;
(2)请根据4月1日、4月2日、4月3日这3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)根据(2)中所得的线性回归方程,预测温差为![]() 时,种子发芽的颗数.
时,种子发芽的颗数.
参考公式: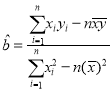 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com