
【题目】已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 的图像与
的图像与![]() 轴围成直角三角形,求
轴围成直角三角形,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)分3段去绝对值解不等式组,再求并;
(2)将y=f(x)去绝对值写出分段函数,根据其图象与x轴围成直角三角形,转化为(a﹣1)(a+1)=﹣1或(a+1)(1﹣a)=﹣1,可解得.
(1)当a=2时,不等式f(x)>1,即|x+1|﹣|2x﹣3|>1,
当x≤﹣1时,原不等式可化为﹣x﹣1+2x﹣3>1,解得x>5,因为x≤﹣1,所以此时原不等式无解;
当﹣1![]() 时,原不等式可化为x+1+2x﹣3>1,解得x>1,所以1<x
时,原不等式可化为x+1+2x﹣3>1,解得x>1,所以1<x![]() ;
;
当x![]() 时,原不等式可化为x+1﹣2x+3>1,解得x<3,所以
时,原不等式可化为x+1﹣2x+3>1,解得x<3,所以![]() x<3.
x<3.
综上,原不等式的解集为{x|1<x<3}.
(2)因为![]() ,所以
,所以![]() ,所以
,所以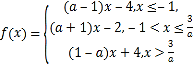 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
当![]() 时,要使得
时,要使得![]() 的图象与
的图象与![]() 轴围成直角三角形,
轴围成直角三角形,
则![]() ,解得
,解得![]() ,舍去;
,舍去;
当![]() 时,
时,![]() 的图象与
的图象与![]() 轴不能围成三角形,不符合题意,舍去;
轴不能围成三角形,不符合题意,舍去;
当![]() 时,要使得
时,要使得![]() 的图象与
的图象与![]() 轴围成直角三角形,
轴围成直角三角形,
则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以
,所以![]() .
.
综上,所求![]() 的值为
的值为![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量.2007年至2018年,某企业连续12年累计研发投入达4100亿元,我们将研发投入与经营收入的比值记为研发投入占营收比.这12年间的研发投入(单位:十亿元)用图中的条形图表示,研发投入占营收比用图中的折线图表示.
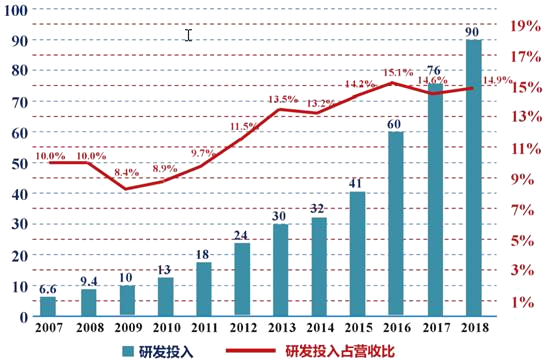
根据折线图和条形图,下列结论错误的是( )
A. 2012﹣2013 年研发投入占营收比增量相比 2017﹣2018 年增量大
B. 该企业连续 12 年研发投入逐年增加
C. 2015﹣2016 年研发投入增值最大
D. 该企业连续 12 年研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进入高中数学竞赛复赛的学生中,高一年级有6人,高二年级有12人, 高三年级有24人,现采用分层抽样的方法从这些学生中抽取7人进行采访.
(1)求应从各年级分别抽取的人数;
(2)若从抽取的7人中再随机抽取2人做进一步了解(注高一学生记为![]() ,高二学生记为
,高二学生记为![]() ,高三学生记为
,高三学生记为![]() ,
,![]() )
)
①列出所有可能的抽取结果;
②求抽取的2人均为高三年级学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入![]() (单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
(单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
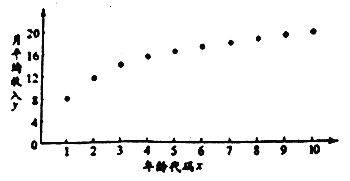
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
附注:①参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为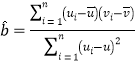 ,
,![]() .
.
③新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税 级数 | 每月应纳税所得额(含税) | 税率 | 每月应纳税所得额(含税) | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的左焦点为
,椭圆的左焦点为![]() ,椭圆上任意点到
,椭圆上任意点到![]() 的最远距离是
的最远距离是![]() ,过直线
,过直线![]() 与
与![]() 轴的交点
轴的交点![]() 任作一条斜率不为零的直线
任作一条斜率不为零的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求椭圆的方程;
(2)求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列推理不属于合情推理的是( )
A. 由铜、铁、铝、金、银等金属能导电,得出一切金属都能导电.
B. 半径为![]() 的圆面积
的圆面积![]() ,则单位圆面积为
,则单位圆面积为![]() .
.
C. 由平面三角形的性质推测空间三棱锥的性质.
D. 猜想数列2,4,8,…的通项公式为![]() .
. ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是
是![]() 上的两个动点,
上的两个动点,![]() ,试问:是否存在定点
,试问:是否存在定点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线![]() :
:![]() (
(![]() ),
),![]() :
:![]() ,
,![]() :
:![]() ,若
,若![]() 与
与![]() 的距离是
的距离是![]() .
.
(1)求a的值:
(2)能否找到一点P,使得点P同时满足下列三个条件:①P是第一象限的点;②点P到![]() 的距离是点P到
的距离是点P到![]() 的距离的
的距离的![]() ;③点P到
;③点P到![]() 的距离与点P到
的距离与点P到![]() 的距离之比是
的距离之比是![]() ,若能,求出点P的坐标,若不能,请说明理由.
,若能,求出点P的坐标,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com