
| A. | $\frac{b^2}{a}$ | B. | $\frac{b^2}{c}$ | C. | $\frac{c^2}{a}$ | D. | $\frac{c^2}{b}$ |
分析 作椭圆,从而可得|PF1|+|PF2|=2a,|PF1|2+|PF2|2=|F1F2|2,从而可得|PF1|•|PF2|=2b2,再由三角形的面积公式求得.
解答 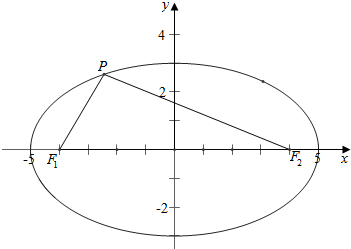 解:由题意作图如右,
解:由题意作图如右,
∵|PF1|+|PF2|=2a,
又∵∠F1PF2=90°,
∴|PF1|2+|PF2|2=|F1F2|2,
∴|PF1|•|PF2|
=$\frac{(|P{F}_{1}|+|P{F}_{2}|)^{2}-(|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2})}{2}$
=$\frac{4{a}^{2}-4{c}^{2}}{2}$=2b2,
设点P到x轴的距离为d,
则|PF1|•|PF2|=|F1F2|•d,
故2b2=2cd,
故d=$\frac{{b}^{2}}{c}$,
故选:B.
点评 本题考查了椭圆的定义的应用及数形结合的思想应用,同时考查了等面积的应用.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com