
【题目】某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.

求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
科目:高中数学 来源: 题型:
【题目】已知D=  ,给出下列四个命题:
,给出下列四个命题:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(2015·新课标Ⅱ)设函数f‘(x)是奇函数f(x)(x![]() R)的导函数,f(-1)=0,当x
R)的导函数,f(-1)=0,当x![]() 0时,xf'(x)-f(x)
0时,xf'(x)-f(x)![]() 0,则使得f(x)
0,则使得f(x)![]() 0成立的x的取值范围是()
0成立的x的取值范围是()
A.(-![]() ,-1)
,-1)![]() (0,1)
(0,1)
B.(-1,0)![]() (1,+
(1,+![]() )
)
C.(-![]() ,-1)
,-1)![]() (-1,0)
(-1,0)
D.(0,1)![]() (1,+
(1,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)已知函数f(x)=x3+ax+![]() , g(x)=-lnx.
, g(x)=-lnx.
(1)当a为何值时,x轴为曲线y=f(x)的切线;
(2)用min{m,n} 表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),,讨论h(x)零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖,求下列问题:(1)求顾客抽奖1次能获奖的概率(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为 X ,求 X 的分布列和数学期望.
(1)(1)求顾客抽奖1次能获奖的概率
(2)(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() , 求
, 求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.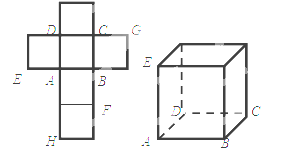
(1)请按字母F , G , H标记在正方体相应地顶点处(不需要说明理由)
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(3)证明:直线DF⊥平面BEG
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=2x , g(x)=x2+ax(其中a![]() R).对于不相等的实数x1, x2 , 设m=
R).对于不相等的实数x1, x2 , 设m=![]() ,n=
,n=![]() .
.
现有如下命题:
(1)对于任意不相等的实数x1, x2 , 都有m>0;
(2)对于任意的a及任意不相等的实数x1, x2 , ,都有n>0;
(3)对于任意的a , 存在不相等的实数x1, x2 , 使得m=n;
(4)对于任意的a , 存在不相等的实数x1, x2 , 使得m=-n.
其中的真命题有 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)某厂用鲜牛奶在某台设备上生产![]() 两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产
两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产![]() 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
(Ⅰ)求Z的分布列和均值;该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com