练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．设集合I={（x，y）|x，y∈Z，0≤x≤5，≤y≤5}则以I中的点为顶点，且位置不同的正方形的个数是55．

    分析 画出：画出点集I={（x，y）|x，y∈Z，0≤x≤5，≤y≤5}中的格点，分别求出以边长为1，2，3，4，5的正方形的个数．

    解答 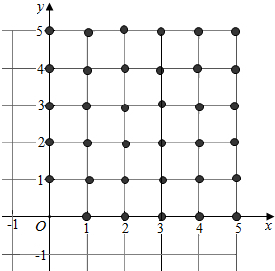解：画出点集I={（x，y）|x，y∈Z，0≤x≤5，≤y≤5}中的格点．如图；
    边长为1个单位长度的正方形，共有5×5=25个，
    边长为2个单位长度的正方形，共有4×4=16个，
    边长为3个单位长度的正方形，共有3×3=9个，
    边长为4个单位长度的正方形，共有2×2=4个，
    边长为5个单位长度的正方形，共有1×1=1个，
    故位置不同的正方形的个数共有25+16+9+4+1=55个，
    故答案为：55．

    点评 解答关键是：利用分类讨论的数学思想求解时，一定要做到分类既不重复，又不遗漏．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．如图，圆E：（x+2）2+y2=4，点F（2，0），动圆P过点F，且与圆E内切于点M，求动圆P的圆心P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．如图，在△ABC中，AB=AC=4，∠BAC=90°，D是边BC的中点，求：
    （1）$\overrightarrow{AB}$在$\overrightarrow{BD}$方向上的投影；
    （2）$\overrightarrow{BD}$在$\overrightarrow{AB}$方向上的投影．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设数列{xn}的通项为xn=$\left\{\begin{array}{l}{\frac{n+1}{\sqrt{n}}，n为奇数}\\{\frac{1}{n}，n为偶数}\end{array}\right.$则{xn}是（　　）
    A．当n→∞时的无穷大量B．当n→∞时的无穷小量
    C．有界变量D．无界变量

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在约束条件$\left\{\begin{array}{l}{x+y≤8}\\{x+y≥2}\\{y≤\frac{1}{2}x+5}\\{x≥0，y≥0}\end{array}\right.$下，求x=2x-y的最小值与最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图所示的茎叶图为甲、乙两家连锁店七天内销售额的某项指标统计：
    （1）求甲家连锁店这项指标的平均数、中位数和众数，并比较甲、乙两该项指标的方差大小；
    （2）每次都从甲、乙两店统计数据中随机各选一个进行对比分析，共选了7次（有放回选取），设选取的两个数据中甲的数据大于乙的数据的次数为X，求X的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=x|x-2a|
    （1）化简f（x）；
    （2）试确定a的取值范围，使函数f（x）在区间[2，+∞）上是单调增函数；
    （3）在（2）的条件下，求函数f（x）在区间[1，2]上的最大值g（a）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．如果函数f（x）=（2m-1）x2+mx+3在实数集R内是单调函数，那么m的值等于$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．函数f（x）=Asin（ωx+ϕ）$（A＞0，ω＞0，0＜ϕ＜\frac{π}{2}）$的部分图象如图所示．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）已知函数$g（x）=sinx•f（\frac{x}{2}）+\sqrt{3}$，$x∈[0，\frac{π}{2}]$，求g（x）的最值及其对应的x值．

    查看答案和解析>>

    同步练习册答案