练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示是一个三棱台ABC－A′B′C′，试用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．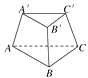

    【答案】解：过A′，B，C三点作一个平面，再过A′，B，C′作一个平面，就把三棱台ABC－A′B′C′分成三部分，形成的三个三棱锥分别是A′－ABC，B－A′B′C′，A′－BCC′.(答案不唯一)
    【解析】本题要结合棱锥的结构特征以及棱台的特征，两者之间的联系。要抓住“每一部分都是一个三棱锥”进行。
    【考点精析】本题主要考查了棱锥的结构特征和棱台的结构特征的相关知识点，需要掌握侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方；①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么①AD⊥MN；②MN∥平面CDE；③MN∥CE；④MN、CE异面．其中假命题的个数为（ ）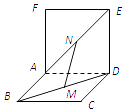

    A.4
    B.3
    C.2
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）、g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＞0，且g（﹣3）=0，则不等式f（x）g（x）＜0的解集是（ ）
    A.（﹣3，0）∪（3，+∞）
    B.（﹣3，0）∪（0，3）
    C.（﹣∞，﹣3）∪（3，+∞）
    D.（﹣∞，﹣3）∪（0，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数g（x）是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＞0时，xg（x）﹣f（x）＜0，则使得f（x）＜0成立的x的取值范围是（ ）
    A.（﹣∞，﹣1）∪（0，1）
    B.（0，1）∪（1，+∞）
    C.（﹣∞，﹣1）∪（﹣1，0）
    D.（﹣1，0）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE= ，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2．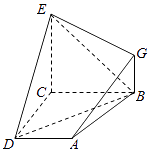
    （1）证明：AG∥平面BDE．
    （2）求平面BDE和平面ADE所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）的定义域[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示

    x

    ﹣1

    0

    2

    4

    5

    F（x）

    1

    2

    1.5

    2

    1

    下列关于函数f（x）的命题；
    ①函数f（x）的值域为[1，2]；
    ②函数f（x）在[0，2]上是减函数
    ③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；
    ④当1＜a＜2时，函数y=f（x）﹣a最多有4个零点．
    其中正确命题的序号是 ．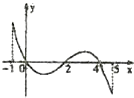

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
    （Ⅰ）证明：PB∥平面AEC；
    （Ⅱ）设二面角D﹣AE﹣C为60°，AP=1，AD= ，求三棱锥E﹣ACD的体积．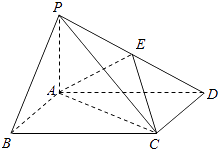

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为 （a为常数，n∈N*）．
    （1）求a1 ， a2 ， a3；
    （2）若数列{an}为等比数列，求常数a的值及an ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校对高一年级学生的数学成绩进行统计，全年级同学的成绩全部介于60分与100分之间，将他们的成绩数据绘制如图所示的频率分布直方图．现从全体学生中，采用分层抽样的方法抽取80名同学的试卷进行分析，则从成绩在[80，100]内的学生中抽取的人数为（ ）

    A.56
    B.32
    C.24
    D.18

    查看答案和解析>>

    同步练习册答案