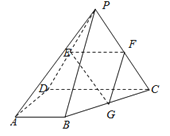
【题目】如图，四棱锥
的底面
是直角梯形,
,
,侧面
底面,
是等边三角形，
，点
分别是棱
的中点 .
（Ⅰ）求证：
平面
；
（Ⅱ）求二面角
的大小；
（Ⅲ）在线段
上存在一点
，使
平面
，且
，求
的值.
【答案】(1)详见解析;(2) 
;(3) 
.
【解析】
试题
(Ⅰ)由题意证得
，结合线面平行的判断定理可得
平面
.
(Ⅱ)建立空间直角坐标系，结合平面的法向量可得二面角
的大小为30°；
(Ⅲ)利用(II)中的空间直角坐标系结合空间向量的坐标表示得到关于实数
的方程，解方程可得.
试题解析：
（Ⅰ）证明：设
是
的中点，连接
∵ 
分别是
的中点
∴ 
，
，∴
∴ 
四点共面
∵ ，
平面
，∴平面
（Ⅱ）
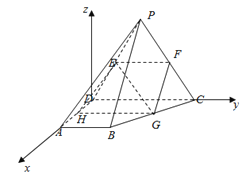
∵ 平面
底面，
∴ 
平面，过点
作
轴与平面
垂直，则轴
平面
以
分别为
轴，
轴建立空间直角坐标系
设平面
的法向量为
，则
设平面的法向量为
，
，
，
，
∴
∴ 
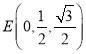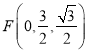
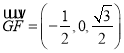
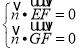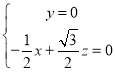
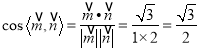
，∴所求二面角大小为.
（Ⅲ）
，
，
，
，设
，
，
∴ 
，
∵ 
平面
，∴
∴ 
， .
科目：高中数学 来源： 题型：
【题目】各项均为正数的数列
的前
项和为
，且对任意正整数，都有
．
（1）求数列的通项公式；
（2）如果等比数列
共有2016项，其首项与公比均为2，在数列的每相邻两项
与
之间插入
个
后，得到一个新的数列
．求数列中所有项的和；
（3）是否存在实数
，使得存在
，使不等式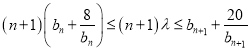
成立，若存在，求实数的范围，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中
.
（1）若曲线
在点
处的切线与直线
平行，求
与
满足的关系；
（2）当
时，讨论
的单调性；
（3）当
时，对任意的
，总有
成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，
是椭圆
：
上的点，过点
的直线的方程为
.
（1）求椭圆的离心率；
（2）当
时，
（i）设直线
与
轴、
轴分别相交于
，
两点，求
的最小值；
（ii）设椭圆的左、右焦点分别为
，
，点
与点关于直线对称，求证：点，，三点共线.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的离心率为
，椭圆的四个顶点围成的四边形的面积为4.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）直线
与椭圆
交于
， 
两点， 
的中点
在圆
上，求
（
为坐标原点）面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】车间将10名技工平均分成甲乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为10.
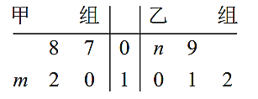
(1)分别求出
,
的值;
(2)质检部门从该车间甲乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率;
(3)根据以上茎叶图和你所学的统计知识,分析两组技工的整体加工水平及稳定性.
(注:方差
,其中
为数据
,
,…,
的平均数).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】谢尔宾斯基三角形（Sierpinskitriangle）是一种分形几何图形，由波兰数学家谢尔宾斯基在1915年提出，它是一个自相似的例子，其构造方法是：
（1）取一个实心的等边三角形（图1）；
（2）沿三边中点的连线，将它分成四个小三角形；
（3）挖去中间的那一个小三角形（图2）；
（4）对其余三个小三角形重复（1）（2）（3）（4）（图3）.
制作出来的图形如图4，图5，….
若图3（阴影部分）的面积为1，则图5（阴影部分）的面积为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【选修4-4，坐标系与参数方程】
在直角坐标系
中，直线
的参数方程为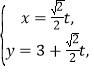
（t为参数），在以O为极点，
轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为
（Ⅰ）求直线的普通方程与曲线C的直角坐标方程；
（Ⅱ）若直线与
轴的交点为P，直线与曲线C的交点为A,B,求
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
