
分析 (Ⅰ)由$y=\frac{1}{2}kx-\frac{1}{80}(1+{k^2}){x^2}(k>0)$,可令y=0,求得x,再由基本不等式可得最大射程;
((Ⅱ)网球发过球网,满足x=8时y>1,解不等式可得k的范围,再由a2k2-40ak+a2+204=0(a≠0),运用判别式非负,解不等式即可得到结论.
解答 解:(Ⅰ)由$\frac{1}{2}$kx-$\frac{1}{80}$(1+k2)x2=0(k>0),
可得:x=$\frac{40k}{1+{k}^{2}}$或x=0,
由x=$\frac{40}{k+\frac{1}{k}}$≤$\frac{40}{2}$=20,当且仅当k=1时取等号.
因此,最大射程为20米;
(Ⅱ)网球发过球网,满足x=8时y>1.
所以4k-$\frac{4}{5}$(1+k2)>1,即4k2-20k+9<0,
因此$\frac{1}{2}$<k<$\frac{9}{2}$,
依题意:关于k的方程$\frac{1}{2}$ka-$\frac{1}{80}$(1+k2)a2=2.55在($\frac{1}{2}$,$\frac{9}{2}$)上有实数解,
即a2k2-40ak+a2+204=0(a≠0),
△=1600a2-4a2(a2+204)≥0
得a≤14,
此时k=$\frac{10}{7}$,球过网了,
所以击球点的横坐标a最大为14.
点评 本题考查函数模型的运用,考查二次函数和二次不等式的解法,同时考查基本不等式的运用:求最值,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
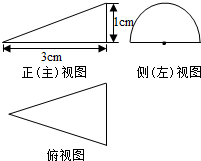 一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )
一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )| A. | $\frac{(\sqrt{10}+1)π}{2}$cm2 | B. | ($\frac{(\sqrt{10}+1)π}{2}$+3)cm2 | C. | ($\frac{π}{2}$+3)cm2 | D. | ($\frac{\sqrt{10}π}{2}$+3)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
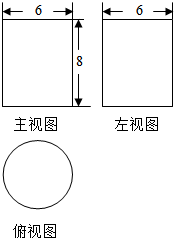 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )| A. | 133π | B. | 100π | C. | 66π | D. | 166π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com