
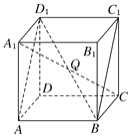
【题目】如图所示,在正方体ABCDA1B1C1D1中,设线段A1C与平面ABC1D1交于点Q,求证:B,Q,D1三点共线.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx![]() )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(1)求函数f(x)的解析式;
(2)求函数y=f(x)的单调增区间;
(3)设α∈(0,![]() ),则f(
),则f(![]() )=2,求α的值.
)=2,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液,已知每投放![]() 且
且![]() 个单位的营养液,它在水中释放的浓度
个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中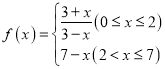 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能持续几天?
(2)若先投放2个单位的营养液,4天后再投放b个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正![]() 边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出
边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出![]() 的值分别为( )
的值分别为( )
(参考数据:![]() )
)

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标(![]() ,
,![]() ),直线l的极坐标方程为ρcos(θ-
),直线l的极坐标方程为ρcos(θ-![]() )=a,.
)=a,.
(1)若点A在直线l上,求直线l的直角坐标方程;
(2)圆C的参数方程为![]() (
(![]() 为参数),若直线
为参数),若直线![]() 与圆C相交的弦长为
与圆C相交的弦长为![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+y2-2x-2y-6=0,以坐标原点O为圆心的圆O与圆M相切.
(1)求圆O的方程;
(2)圆O与x轴交于E,F两点,圆O内的动点D使得DE,DO,DF成等比数列,求![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.
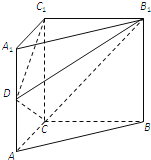
(1)求异面直线DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为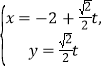 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com