解:(I)f′(x)=3mx
2-1,
由题意得f′(2)=12m-1=3,解得m=

,
所以f(x)=

x
3-x+

,
所以n=f(2)=1;
(II)因为F(x)=f(x)+g(x)=
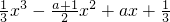
,
所以F′(x)=x
2-(a+1)x+a=(x-1)(x-a),令F′(x)=0得x=1或x=a,
当0<a<1时,令F′(x)>0得0<x<a,或1<x<2,令F′(x)<0得a<x<1,
因为F(x)在[0,2]上有最大值 1,F(2)=1,所以F(a)≤1,即a
3-3a
2+4≥0,
令g(a)=a
3-3a
2+4,则g′(a)=3a
2-6a=3a(a-2),所以g′(a)<0,
所以g(a)>g(1)=0,所以0<a<1;
当a=1时,F′(x)=x
2-2x+1=(x-1)
2≥0,F(x)≤F(2)=1成立;
当1<a<2时,令F′(x)>0得0<x<1或a<x<2,令F′(x)<0得1<x<a,F(2)=1,
因为F(x)在[0,2]上有最大值 1,所以F(1)≤1,即
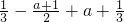
≤1,解得a
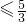
,所以1<a
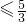
;
当a≥2时,由F(x)的单调性知F(x)
max=F(1)>F(2),故不成立;
综上,实数a的范围是0<a
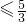
.
分析:(I)由N点处切线斜率为3可得f′(2)=3,由此可得m值,则n=f(2),算出即可;
(II)求出F′(x),按照0<a<1,a=1,1<a<2,a≥2进行讨论:研究函数F(x)在[0,2]上的单调性、极值,根据其最大值为1可得不等式,解出即可;
点评:本题考查利用导数研究函数在某点处的切线方程、函数在闭区间上的最值,考查分类讨论思想,考查学生解决问题的能力,综合性强,难度大.

 ,以点N(2,n)为切点的该图象的切线的斜率为3
,以点N(2,n)为切点的该图象的切线的斜率为3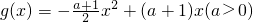 ,若F(x)=f(x)+g(x)在[0,2]上有最大值 1,试求实数a的取值范围.
,若F(x)=f(x)+g(x)在[0,2]上有最大值 1,试求实数a的取值范围. ,
, x3-x+
x3-x+ ,
,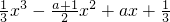 ,
,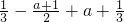 ≤1,解得a
≤1,解得a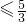 ,所以1<a
,所以1<a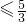 ;
;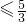 .
.

 备战中考寒假系列答案
备战中考寒假系列答案