练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】图中，小方格是边长为1的正方形，图中粗线画出的是某几何体的三视图，且该几何体的顶点都在同一球面上，则该几何体的外接球的表面积为（　　）

    A.32π
    B.48π
    C.50π
    D.64π

    【答案】C
    【解析】解：由三视图可知该几何体是一个底面是矩形的四棱锥，

    记该几何体的外接球球心为O，半径R=OA，

    则PA= × = ，OP=R﹣ ，

    所以OA2=OP2+AP2，

    又因为OP2= = ，

    所以R2= + ，解得：R= ，

    所以所求面积S=4π×R2=4π× =50π，

    所以答案是：C．

    【考点精析】关于本题考查的由三视图求面积、体积，需要了解求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的前n项和为Sn ， 且 （a∈N+）．
    （1）求a的值及数列{an}的通项公式；
    （2）设 ，求{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】集合L={l|l与直线y=x相交，且以交点的横坐标为斜率}．若直线l′∈L，点P（﹣1，2）到直线l′的最短距离为r，则以点P为圆心，r为半径的圆的标准方程为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学为研究函数 的性质，构造了如图所示的两个边长为1的正方形ABCD和BEFC，点P是边BC上的一个动点，设CP=x，则AP+PF=f（x）．请你参考这些信息，推知函数f（x）的值域是 ．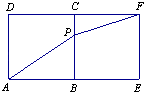

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx+x2 ．
    （Ⅰ）若函数g（x）=f（x）﹣ax在其定义域内为增函数，求实数a的取值范围；
    （Ⅱ）在（Ⅰ）的条件下，若a＞1，h（x）=e3x﹣3aexx∈[0，ln2]，求h（x）的极小值；
    （Ⅲ）设F（x）=2f（x）﹣3x2﹣kx（k∈R），若函数F（x）存在两个零点m，n（0＜m＜n），且2x0=m+n．问：函数F（x）在点（x0 ， F（x0））处的切线能否平行于x轴？若能，求出该切线方程；若不能，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知m＞1，直线l：x﹣my﹣ =0，椭圆C： +y2=1，F1、F2分别为椭圆C的左、右焦点．
    （Ⅰ）当直线l过右焦点F2时，求直线l的方程；
    （Ⅱ）设直线l与椭圆C交于A、B两点，△AF1F2 ， △BF1F2的重心分别为G、H．若原点O在以线段GH为直径的圆内，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是公差为2的等差数列，数列{bn}满足 ，若n∈N*时，anbn+1﹣bn+1=nbn ．
    （Ⅰ）求{bn}的通项公式；
    （Ⅱ）设 ，求{Cn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=aex﹣2x﹣2a，且a∈[1，2]，设函数f（x）在区间[0，ln2]上的最小值为m，则m的取值范围是（　　）
    A.[﹣2，﹣2ln2]
    B.[﹣2，﹣ ]
    C.[﹣2ln2，﹣1]
    D.[﹣1，﹣ ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx﹣kx+k（k∈R）．
    （Ⅰ）求f（x）在[1，2]上的最小值；
    （Ⅱ）若 ，对x∈（﹣1，1）恒成立，求正数a的最大值．

    查看答案和解析>>

    同步练习册答案