
 =1(a>b>0)与一等轴双曲线相交,M是其中一个交点,并且双曲线的顶点是该椭圆的焦点F1,F2,双曲线的焦点是椭圆的顶点A1,A2,△MF1F2的周长为4(
=1(a>b>0)与一等轴双曲线相交,M是其中一个交点,并且双曲线的顶点是该椭圆的焦点F1,F2,双曲线的焦点是椭圆的顶点A1,A2,△MF1F2的周长为4( +1).设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1).设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
 +1),解方程组即可求得椭圆的方程,等轴双曲线的顶点是该椭圆的焦点可求得该双曲线的方程;
+1),解方程组即可求得椭圆的方程,等轴双曲线的顶点是该椭圆的焦点可求得该双曲线的方程; (x-2),联立直线和椭圆方程,利用韦达定理,即可求得|AB|,|CD|,代入|AB|+|CD|=λ|AB|•|CD|,求得λ的值.
(x-2),联立直线和椭圆方程,利用韦达定理,即可求得|AB|,|CD|,代入|AB|+|CD|=λ|AB|•|CD|,求得λ的值. =
= ,得a=
,得a= c,
c, +1),所以可解得a=2
+1),所以可解得a=2 ,c=2,
,c=2, ,
, ;
; ,k2=
,k2= ,
,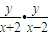 =
= ,
, ,即y2=x2-4,
,即y2=x2-4, =1;
=1; (x-2),
(x-2), ,x1•x2=
,x1•x2= ,
, |x1-x2|=
|x1-x2|=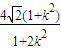 ,
,
 =
= =
=
 ,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
,使得|AB|+|CD|=λ|AB|•|CD|恒成立.

科目:高中数学 来源:2012-2013学年辽宁省铁岭市开原市高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 =1(a>b>0)与过A(2,0),B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过A(2,0),B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
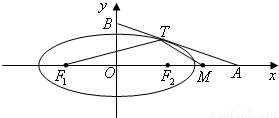
查看答案和解析>>
科目:高中数学 来源:2009-2010学年陕西省延安市实验中学高二(下)期中数学试卷(理科)(解析版) 题型:解答题
 如图,椭圆
如图,椭圆 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e= .
.查看答案和解析>>
科目:高中数学 来源:2011年四川省南充市高考数学零诊试卷(文科)(解析版) 题型:解答题
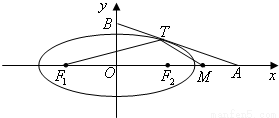 如图,椭圆
如图,椭圆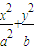 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=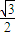 .
.查看答案和解析>>
科目:高中数学 来源:2006年浙江省高考数学试卷(理科)(解析版) 题型:解答题
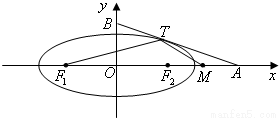 如图,椭圆
如图,椭圆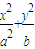 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=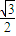 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com