
 根据如图所示的求公约数方法的程序框图,输入m=2146,n=1813,则输出的m的值为
根据如图所示的求公约数方法的程序框图,输入m=2146,n=1813,则输出的m的值为 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
 )图象上所有点向右平移
)图象上所有点向右平移 个单位,再将所得图象的横坐标变为原来的
个单位,再将所得图象的横坐标变为原来的 倍(纵坐标不变),得图象的解析式是y=sin(ωx+ψ)(ω>0,|ψ|<π),则
倍(纵坐标不变),得图象的解析式是y=sin(ωx+ψ)(ω>0,|ψ|<π),则 ,ψ=-
,ψ=-


查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 =(
=( sin2x-1,cosx),
sin2x-1,cosx), =(1,2cosx),设函数
=(1,2cosx),设函数 .
.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
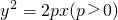 的焦点F,且交抛物线于P、Q两点,由P、Q分别向准线引垂线PR、QS,垂足分别为R、S,如果|PF|=a,|QF|=b,M为RS的中点,则|MF|=________.
的焦点F,且交抛物线于P、Q两点,由P、Q分别向准线引垂线PR、QS,垂足分别为R、S,如果|PF|=a,|QF|=b,M为RS的中点,则|MF|=________.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校随机抽取100名学生高中学业水平考试的X科成绩,并将成绩分成5组,得到频率分布表(部分)如下.
某校随机抽取100名学生高中学业水平考试的X科成绩,并将成绩分成5组,得到频率分布表(部分)如下.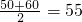 ),估计该校学生本次学业水平测试X科的平均分;
),估计该校学生本次学业水平测试X科的平均分;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com