
【题目】已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() .
.
(Ⅰ)若原点到直线x+y-b=0的距离为![]() ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设过椭圆的右焦点且倾斜角为45°的直线l和椭圆交于A,B两点,对于椭圆上任意一点M,总存在实数λ、μ,使等式![]() 成立,求λ2+μ2的值.
成立,求λ2+μ2的值.
【答案】(Ⅰ) ![]() (Ⅱ)λ2+μ2=1
(Ⅱ)λ2+μ2=1
【解析】试题分析:(1)由点到直线的距离公式与![]() ,可得a,b,c及椭圆方程。(2)设A(x1,y1),B(x2,y2),椭圆方程为x2+3y2=3b2,设直线方程为y=x-c,直线与椭圆方程组方程组得到A,B点坐标的韦达定理,由等式
,可得a,b,c及椭圆方程。(2)设A(x1,y1),B(x2,y2),椭圆方程为x2+3y2=3b2,设直线方程为y=x-c,直线与椭圆方程组方程组得到A,B点坐标的韦达定理,由等式![]() ,可得M(
,可得M(![]() ),把A,B,M三点坐标代入椭圆方程,及韦达可得λ2+μ2=1.
),把A,B,M三点坐标代入椭圆方程,及韦达可得λ2+μ2=1.
试题解析:(Ⅰ)∵d=![]() =
=![]() ,∴b=2.
,∴b=2.
又∵e=![]() =
=![]() ,∴e2=
,∴e2=![]() ,
,
∴b2=a2-c2=![]() a2=4,得a2=12,b2=4.
a2=4,得a2=12,b2=4.
∴椭圆的方程为![]() .
.
(Ⅱ)∵e=![]() =
=![]() ,∵a2=b2+c2,
,∵a2=b2+c2,
∴a2=3b2,∴椭圆方程为x2+3y2=3b2,
又直线方程为y=x-c,
联立![]() 4x2-6cx+3c2-3b2=0,
4x2-6cx+3c2-3b2=0,
设A(x1,y1),B(x2,y2),则x1+x2=![]() c,x1x2=
c,x1x2=![]() =
=![]() c2,
c2,
显然![]() 与
与![]() 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量![]() ,有且只有一对实数λ,μ,使得等式
,有且只有一对实数λ,μ,使得等式![]() 成立.
成立.
设M(x,y),则由![]() 得
得![]() ,
,
代入椭圆方程整理得λ2![]() +μ2
+μ2![]() +2λμ(x1x2+3y1y2)=3b2.
+2λμ(x1x2+3y1y2)=3b2.
又∵![]() =3b2,
=3b2, ![]() =3b2,
=3b2,
x1x2+3y1y2=4x1x2-3c(x1+x2)+3c2=![]() c2-
c2-![]() c2+3c2=0,
c2+3c2=0,
∴λ2+μ2=1.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0.且a2,a5,a14分别是等比数列{bn}的b2,b3,b4.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有![]() 成立,求c1+c2+…+c2016的值.
成立,求c1+c2+…+c2016的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点![]() ,抛物线上的点
,抛物线上的点![]() ,过点B作直线AP的垂线,垂足为Q.
,过点B作直线AP的垂线,垂足为Q.
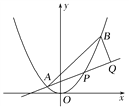
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
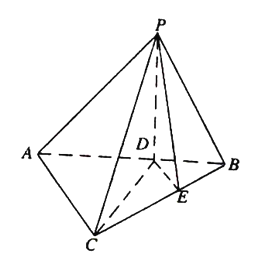
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.

(Ⅰ)求证:平面AB1M⊥平面A1ABB1;
(Ⅱ)过点C作一截面与平面AB1M平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=![]() ,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com