【题目】某调查机构对本市小学生课业负担情况进行了调查，设平均每人每天做作业的时间为x分钟．有1000名小学生参加了此项调查，调查所得数据用程序框图处理，若输出的结果是680，则平均每天做作业的时间在0～60分钟内的学生的频率是（ ）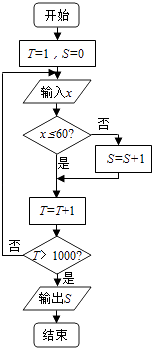 
A.680
B.320
C.0.68
D.0.32
【答案】D
【解析】做！
解：分析程序中各变量、各语句的作用，
再根据流程图所示的顺序，可知：
该程序的作用是统计1000名中学生中，
平均每天做作业的时间不在0～60分钟内的学生的人数．
由输出结果为680
则平均每天做作业的时间在0～60分钟内的学生的人数为1000﹣680=320
故平均每天做作业的时间在0～60分钟内的学生的频率P= 
=0.32
所以答案是：0.32
【考点精析】解答此题的关键在于理解程序框图的相关知识，掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．
科目：高中数学 来源： 题型：
【题目】设向量 
=（4cosα，sinα）， 
=（sinβ，4cosβ）， 
=（cosβ，﹣4sinβ）
（1）若 与 ﹣2 垂直，求tan（α+β）的值；
（2）若β∈（﹣ 
]，求| 
|的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆经过点
，点
是椭圆上在第一象限的点，直线
交
轴于点
，直线
交
轴于点
.
（Ⅰ）求椭圆的标准方程和离心率；
（Ⅱ）是否存在点
，使得直线
与直线
平行？若存在，求出点
的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=sin（2x+ 
）+tan 
cos2x．
（1）求f（x）的最小正周期及其图象的对称轴方程；
（2）求函数f（x）在区间（0， 
）上的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数φ(x)＝
，a为正常数．
(Ⅰ)若f(x)＝ln x＋φ(x)，且a＝4，讨论函数f(x)的单调性；
(Ⅱ)若g(x)＝|ln x|＋φ(x)，且对任意x1，x2∈(0，2]，x1≠x2都有
(ⅰ)求实数a的取值范围；
(ⅱ)求证：当x∈(0，2]时，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线 
的参数方程为 
，曲线 
的参数方程为 
，设直线 与曲线 交于两点 
,
（1）求 
；
（2）设 
为曲线 上的一点，当 
的面积取最大值时，求点 的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线 
（t为参数）， 
（ 
为参数）．
（1）化 
的方程为普通方程；
（2）若 
上的点对应的参数为 
，Q为 
上的动点，求PQ中点M到直线（t为参数）距离的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数y=x3与y=（ 
）x﹣2的图象的交点为（x0 ， y0），则x0所在的区间是（ ）
A.（0，1）
B.（1，2）
C.（2，3）
D.（3，4）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
