
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.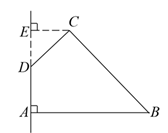
S表面=(60+4 )π.V=
)π.V=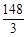 π.
π.
解析试题分析:该图形旋转后是一个圆台除去一个倒放的圆锥,
则S表面=S下底面+S台侧面+S锥侧面 ,
设圆台上,下地面半径是r1,r2,
则 S表面=π×r22+π×(r2+r1)×5+π×r1×CD
V=V台-V锥=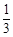 π(
π(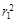 +r1r2+
+r1r2+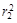 )AE-
)AE-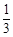 πr2DE,将数据代入计算即可。
πr2DE,将数据代入计算即可。
试题解析:
如图,设圆台上,下地面半径是r1,r2,过C点作CF⊥AB,由∠ADC=135°,CE⊥AD, CD=2 得∠EDC=45°,r1=" CE=" 2,
得∠EDC=45°,r1=" CE=" 2,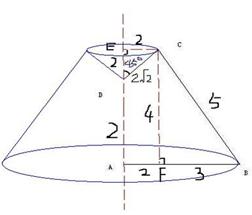
则CF=4,BF=3,CF⊥AB,得BC=5,r2=" AB=" 5,
∴S表面=S下底面+S台侧面+S锥侧面
=π×r22+π×(r2+r1)×5+π×r1×CD
=π×52+π×(2+5)×5+π×2×2
=(60+4 )π.
)π.
V=V台-V锥
=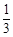 π(
π(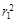 +r1r2+
+r1r2+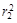 )AE-
)AE-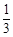 π
π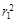 DE
DE
=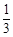 π(
π(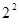 +2×5+
+2×5+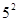 )4-
)4-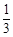 π
π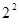 ×2
×2
=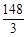 π.
π.
考点:圆台,圆锥的表面积和体积.


科目:高中数学 来源: 题型:解答题
如图,圆柱的轴截面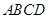 为正方形,
为正方形,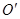 、
、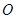 分别为上、下底面的圆心,
分别为上、下底面的圆心,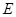 为上底面圆周上一点,已知
为上底面圆周上一点,已知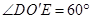 ,圆柱侧面积等于
,圆柱侧面积等于 .
.
(1)求圆柱的体积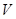 ;
;
(2)求异面直线 与
与 所成角
所成角 的大小.
的大小.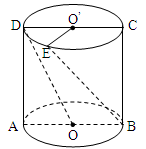
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,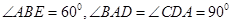 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC 平面
平面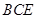 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com