
【题目】已知 ![]() ,则cosα﹣sinα= , sin2α= .
,则cosα﹣sinα= , sin2α= .
【答案】![]() 或
或 ![]() ;
;![]() 或﹣1
或﹣1
【解析】解:①已知 (cosα+sinα)(cosα﹣sinα)= ![]() ,
,
若cosα+sinα≠0,则cosα﹣sinα= ![]() .
.
若cosα+sinα=0,则cosα=﹣sinα,tanα=﹣1,
此时,cosα= ![]() ,sinα=﹣
,sinα=﹣ ![]() ,cosα﹣sinα=
,cosα﹣sinα= ![]() ;
;
或cosα=﹣ ![]() ,sinα=
,sinα= ![]() ,cosα﹣sinα=﹣
,cosα﹣sinα=﹣ ![]() .
.
综合可得,cosα﹣sinα= ![]() 或±
或± ![]() .
.
②当cosα﹣sinα= ![]() ,则由cos2α+sin2α=1,可得cosα=
,则由cos2α+sin2α=1,可得cosα= ![]() ,sinα=
,sinα= ![]() ;
;
或cosα= ![]() ,sinα=
,sinα= ![]() ,
,
∴sin2α=2sinαcosα= ![]() .
.
当cosα+sinα=0,sin2α=2sinαcosα=﹣1,综合可得sin2α= ![]() 或﹣1,
或﹣1,
所以答案是: ![]() 或
或 ![]() ;
; ![]() 或﹣1.
或﹣1.
【考点精析】掌握同角三角函数基本关系的运用是解答本题的根本,需要知道同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ.
(1)求出圆C的直角坐标方程;
(2)已知圆C与x轴相交于A,B两点,直线l:y=2x关于点M(0,m)(m≠0)对称的直线为l'.若直线l'上存在点P使得∠APB=90°,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点;
(1)若∠BFD=90°,△ABD的面积为 ![]() ,求p的值及圆F的方程;
,求p的值及圆F的方程;
(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱A1B1C1D1﹣ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1 . (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
(1)求证:BF⊥平面ACFD;
(2)求直线BD与平面ACFD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c.已知acosB﹣c= ![]() .
.
(1)求角A的大小;
(2)若b﹣c= ![]() ,a=3+
,a=3+ ![]() ,求BC边上的高.
,求BC边上的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点. 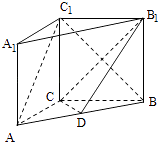
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体EF﹣ABCD中,ABCD,ABEF均为直角梯形, ![]() ,DCEF为平行四边形,平面DCEF⊥平面ABCD.
,DCEF为平行四边形,平面DCEF⊥平面ABCD. 
(1)求证:DF⊥平面ABCD;
(2)若△ABD是等边三角形,且BF与平面DCEF所成角的正切值为 ![]() ,求二面角A﹣BF﹣C的平面角的余弦值.
,求二面角A﹣BF﹣C的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数x2=4y的焦点是F,直线l与抛物线交于A,B两点.
(1)若直线l过焦点F且斜率为1,求线段AB的长;
(2)若直线l与y轴不垂直,且|FA|+|FB|=3.证明:线段AB的中垂线恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com