
【题目】设函数f(x)=ax3﹣3x+1(x∈R),若对于任意的x∈[﹣1,1]都有f(x)≥0成立,则实数a的值为 .
【答案】4
【解析】解:由题意,f′(x)=3ax2﹣3, 当a≤0时3ax2﹣3<0,函数是减函数,f(0)=1,只需f(1)≥0即可,解得a≥2,与已知矛盾,
当a>0时,令f′(x)=3ax2﹣3=0解得x=± ![]() ,
,
①当x<﹣ ![]() 时,f′(x)>0,f(x)为递增函数,
时,f′(x)>0,f(x)为递增函数,
②当﹣ ![]() <x<
<x< ![]() 时,f′(x)<0,f(x)为递减函数,
时,f′(x)<0,f(x)为递减函数,
③当x> ![]() 时,f(x)为递增函数.
时,f(x)为递增函数.
所以f( ![]() )≥0,且f(﹣1)≥0,且f(1)≥0即可
)≥0,且f(﹣1)≥0,且f(1)≥0即可
由f( ![]() )≥0,即a
)≥0,即a ![]() ﹣3
﹣3 ![]() +1≥0,解得a≥4,
+1≥0,解得a≥4,
由f(﹣1)≥0,可得a≤4,
由f(1)≥0解得2≤a≤4,
综上a=4为所求.
所以答案是:4.
【考点精析】关于本题考查的函数的最大(小)值与导数,需要了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】甲乙两机床同时加工直径为100mm的零件,为检验质量,随机从中各抽取5件,测量结果如图,请说明哪个机床加工的零件较好?
甲 | 99 | 100 | 98 | 100 | 103 |
乙 | 99 | 100 | 102 | 99 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xex﹣ax2﹣x,a∈R.
(1)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若对x≥1时,恒有f(x)≥xex+ax2成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1. 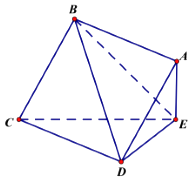
(1)求证:AB∥平面CDE;
(2)求证:DE⊥平面ABE;
(3)求点A到平面BDE的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com