
���� ��1��Ӧ���������ڣ��ٳ˷������ӦΪ$\sqrt{2}$��
��2����֪loga$\frac{2}{3}$��1���Ե���a�������ۣ���a��1ʱ�����������0��a��1ʱ����֪loga$\frac{2}{3}$��logaa���ɵ�a��$\frac{2}{3}$��
��3������y=2x���У�ʹx��y��ȡ�෴���ɵã�-y=2-x����y=-2-x��
��4������f��x��=$\frac{1}{{\sqrt{m{x^2}+mx+1}}}$�Ķ�������R����mx2+mx+1��0���������Զ�����ϵ�����ۣ��ɵá���0����m=0��
��5������y=ln��-x2+x���Ķ�����Ϊ��0��1������������Ӧ�ڶ������ڣ�
��� �⣺��1��Ӧ���������ڣ��ٳ˷������ӦΪ$\sqrt{2}$���ʴ���
��2����֪loga$\frac{2}{3}$��1����a��1ʱ�����������0��a��1ʱ����֪loga$\frac{2}{3}$��logaa���ɵ�a��$\frac{2}{3}$���ʴ���
��3������y=2x���У�ʹx��y��ȡ�෴���ɵã�-y=2-x����y=-2-x������ȷ��
��4������f��x��=$\frac{1}{{\sqrt{m{x^2}+mx+1}}}$�Ķ�������R����mx2+mx+1��0��������ɵá���0����m=0���ʴ���
��5������y=ln��-x2+x���Ķ�����Ϊ��0��1���ʴ���
�ʴ�Ϊ��3����
���� �����˳˷������㣬���������������������⣬ͼ��ĶԳ����⣬���κ�������������⣮���ڻ������ͣ�Ӧ�������գ�


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�����ԲΪ��O���ӳ�CB��Q�����ӳ�QA��P��ʹ��QC2-QA2=BC•QC��
��ͼ����ABC�����ԲΪ��O���ӳ�CB��Q�����ӳ�QA��P��ʹ��QC2-QA2=BC•QC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����HΪ��ǡ�ABC�Ĵ��ģ�����H��BH�Ĵ��ߣ���AB����D������H��CH�Ĵ��ߣ���AC���ڵ�E����C��BC�Ĵ��ߣ���ֱ��DE���ڵ�F��֤��FH=FC��
��ͼ����HΪ��ǡ�ABC�Ĵ��ģ�����H��BH�Ĵ��ߣ���AB����D������H��CH�Ĵ��ߣ���AC���ڵ�E����C��BC�Ĵ��ߣ���ֱ��DE���ڵ�F��֤��FH=FC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
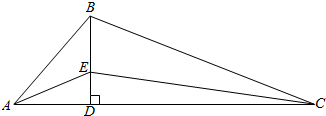
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��N | B�� | N��P | C�� | M��Q | D�� | N��Q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | 6 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com