
| 5 |
| 5 |
| 5 |
|
| 5 |
| 5 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 5 |


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
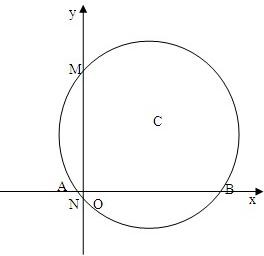 已知圆C满足:
已知圆C满足:查看答案和解析>>
科目:高中数学 来源: 题型:
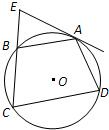 附加题:
附加题:
|
|
| 12 |
| 3cos2θ+4sin2θ |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
查看答案和解析>>
科目:高中数学 来源:新疆乌鲁木齐一中2012届高三上学期第三次月考数学理科试题 题型:013
已知x,y满足
![]() ,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为
,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为
45
36
30
27
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高一第一学期期末测试数学 题型:解答题
(本小题12分)已知圆C满足(1)截y轴所得弦MN长为4;(2)被x轴分成两段圆弧,其弧 长之比为3:1,且圆心在直线y=x上,求圆C的方程。
(为方便学生解答,做了一种情形的辅助图形)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com