Question

在△ABC中，角A，B，C的对边长分别为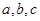，已知向量，，．
（1）求角A的值；
（2）若=2，=2，求c的值．

Answer 1

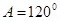(1)；（2）.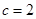

解析试题分析：（1)先用数量积的概念转化为三角函数的形式，寻求角与角之间的关系，化非特殊角为特殊角；正确灵活运用公式，通过三角变换消去或约去一些非特殊角的三角函数值，注意题中角的范围；（2）掌握一些常规技巧：“1”的代换，和积互化等，异名三角函数化为同名三角函数，异角化为同角，异次化为同次，切化弦，特殊角与特殊角的三角函数互化；（3）在三角形中，处理三角形的边角关系时，一般全部化成角的关系，或全部化成边的关系，解决三角形问题时，注意角的范围.
试题解析：（1）由于向量，，．
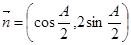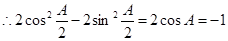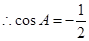，，又，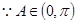
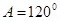
由于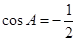，由余弦定理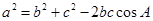当，代入当，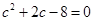
由于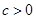解得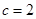
考点：（1）平面向量数量积的运算；（2）二倍角公式的应用；（3)余弦定理的应用.