
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点
=1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点 ![]() .
.
(1)求椭圆C的方程;
(2)设M,N为椭圆C上不同的两点,A,B分别为椭圆C上的左右顶点,直线MN既不平行与坐标轴,也不过椭圆C的右焦点F,若∠AFM=∠BFN,求证:直线MN过定点.
【答案】
(1)
解:由题意可知:短轴一个端点到右焦点F的距离为2,则a=2,
将 ![]() 代入椭圆方程可得
代入椭圆方程可得 ![]() ,解得:b2=1,
,解得:b2=1,
∴椭圆的标准方程: ![]()
(2)
证明:由(1)可知:F( ![]() ,0),
,0),
设直线MN的方程y=k1x+m,(k≠0),M(x1,y1),N(x2,y2).
则 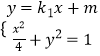 ,整理得:(1+2k12)x2+8k1mx+4m2﹣4=0,
,整理得:(1+2k12)x2+8k1mx+4m2﹣4=0,
x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由∠AFM=∠BFN,则kFM+kFN=0, ![]() +
+ ![]() =0,
=0,
(k1x1+m)(x2﹣ ![]() )+(k1x2+m)(x1﹣
)+(k1x2+m)(x1﹣ ![]() )=0,
)=0,
整理得:2k1x1x2﹣(m﹣ ![]() k1)(x1+x2)﹣2
k1)(x1+x2)﹣2 ![]() m=0,
m=0,
则2k1× ![]() ﹣(m﹣
﹣(m﹣ ![]() k1)(﹣
k1)(﹣ ![]() )﹣2
)﹣2 ![]() m=0,
m=0,
解得:m=﹣ ![]() k1,
k1,
∴直线MN的方程为y=k1(x﹣ ![]() ),
),
则直线MN过定点( ![]() ,0)
,0)
【解析】(1)由题意可知:a=2,将点代入椭圆方程,即可求得b的值,即可求得椭圆方程;(2)设直线MN的方程y=k1x+m,代入椭圆方程,由韦达定理,及kFM+kFN=0,即可求得m=﹣ ![]() k1 , 直线MN的方程为y=k1(x﹣
k1 , 直线MN的方程为y=k1(x﹣ ![]() ),则直线MN过定点(
),则直线MN过定点( ![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点M的极坐标为 ![]() ,圆C的参数方程为
,圆C的参数方程为 ![]() (α为参数).
(α为参数).
(1)直线l过M且与圆C相切,求直线l的极坐标方程;
(2)过点P(0,m)且斜率为 ![]() 的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为假命题:
”的逆否命题为假命题:
②命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
③若“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,则
”为假命题,则![]() 为真命题,
为真命题,![]() 为假命题;
为假命题;
④函数![]() 有极值的充要条件是
有极值的充要条件是![]() 或
或![]() .
.
其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
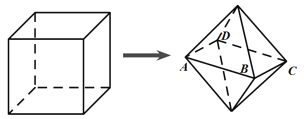
【题目】如图,棱长为1(单位:![]() )的正方体木块经过适当切割,得到几何体
)的正方体木块经过适当切割,得到几何体![]() ,已知几何体
,已知几何体![]() 由两个底面相同的正四棱锥组成,底面
由两个底面相同的正四棱锥组成,底面![]() 平行于正方体的下底面,且各顶点均在正方体的面上,则几何体
平行于正方体的下底面,且各顶点均在正方体的面上,则几何体![]() 体积的取值范围是________(单位:
体积的取值范围是________(单位:![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A. 22种 B. 24种 C. 25种 D. 27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生参加了“铅球”和“立定跳远”两个科目的体能测试,每个科目的成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级,分别对应5分,4分,3分,2分,1分,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为
五个等级,分别对应5分,4分,3分,2分,1分,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为![]() 的学生有8人.
的学生有8人.

(Ⅰ)求该班学生中“立定跳远”科目中成绩为![]() 的人数;
的人数;
(Ⅱ)若该班共有10人的两科成绩得分之和大于7分,其中有2人10分,3人9分,5人8分.从这10人中随机抽取两人,求两人成绩之和![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() :
:![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求![]() 的长;
的长;
(Ⅱ)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立的极坐标系中,设点
轴的正半轴为极轴建立的极坐标系中,设点![]() 的极坐标为
的极坐标为![]() ,求点
,求点![]() 到线段
到线段![]() 中点
中点![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1 , x2 , 当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1 , y2 , 使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.
则 ① , ②
, ② ,
,
③ , ④
, ④![]() ,
,
四个函数中为不严格增函数的是 ,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com