
(本题14分)一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到黑球的概率是![]() ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是![]() 。
。
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的数学期望
的数学期望![]() 。
。
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于![]() 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。
(Ⅰ)(i)5
(ii)![]()
(Ⅱ)证明见解析。
本题主要考查排列组合、对立事件、相互独立事件的概率和随机变量分布列和数学期望等概念,同时考查学生的逻辑思维能力和分析问题以及解决问题的能力.满分14分。
(Ⅰ)解:(i)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,
设袋中白球的个数为![]() ,则
,则![]() ,
,
得到![]() ,故白球有5个。
,故白球有5个。
(ii)随机变量![]() 的取值为0,1,2,3,分布列是
的取值为0,1,2,3,分布列是
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
![]() 的数学期望
的数学期望
![]() 。
。
(Ⅱ)证明:设袋中有![]() 个球,其中
个球,其中![]() 个黑球,由题意得
个黑球,由题意得![]() ,
,
所以![]() ,
,![]() ,故
,故![]() 。
。
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则
![]()
![]() 。
。
所以白球的个数比黑球多,白球个数多于![]() ,红球的个数少于
,红球的个数少于![]() 。
。
故袋中红球个数最少。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010-2011学年浙江省温州市高三五校联考数学理卷 题型:解答题
(本题满分14分)某超市为促销商品,特举办“购物有奖100﹪中奖”活动,凡消费者在该超市购物满100元,享受一次摇奖机会,购物满200元,享受两次摇奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是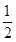
(Ⅰ)求:摇奖两次,均获得一等奖的概率;
(Ⅱ)某消费者购物满200元,摇奖后所得奖金为X元,试求X的分布列与期望;
(Ⅲ)若超市同时举行购物八八折让利于消费者活动(打折后不再享受摇奖),某消费者刚好消费200元,请问他是选择摇奖还是选择打折比较划算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com