
【题目】天津市某中学为全面贯彻“五育并举,立德树人”的教育方针,促进学生各科平衡发展,提升学生综合素养.该校教务处要求各班针对薄弱学科生成立特色学科“兴趣学习小组”(每位学生只能参加一个小组),以便课间学生进行相互帮扶.已知该校某班语文数学英语三个兴趣小组学生人数分别为10人10人15人.经过一段时间的学习,上学期期中考试中,他们的成绩有了明显进步.现采用分层抽样的方法从该班的语文,数学,英语三个兴趣小组中抽取7人,对期中考试这三科成绩及格情况进行调查.
(1)应从语文,数学,英语三个兴趣小组中分别抽取多少人?
(2)若抽取的7人中恰好有5人三科成绩全部及格,其余2人三科成绩不全及格.现从这7人中随机抽取4人做进一步的调查.
①记![]() 表示随机抽取4人中,语文,数学,英语三科成绩全及格的人数,求随机变量
表示随机抽取4人中,语文,数学,英语三科成绩全及格的人数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
②设![]() 为事件“抽取的4人中,有人成绩不全及格”,求事件
为事件“抽取的4人中,有人成绩不全及格”,求事件![]() 发生的概率.
发生的概率.
【答案】(1)语文数学英语三个兴趣小组中分别抽取![]() 人
人![]() 人
人![]() 人.(2)①分布列答案见解析,数学期望
人.(2)①分布列答案见解析,数学期望![]() ,②概率为
,②概率为![]() .
.
【解析】
(1)由语文数学英语三个兴趣小组的人数之比为![]() ,利用分层抽样方法确定抽取的人数.
,利用分层抽样方法确定抽取的人数.
(2)①根据抽取的7人中恰好有5人三科成绩全部及格,其余2人三科成绩不全及格.得到随机抽取4人中,语文,数学,英语三科成绩全及格的人数可能![]() 人,再求得相应概率,列出分布列,再求期望.②设事件
人,再求得相应概率,列出分布列,再求期望.②设事件![]() 为“抽取的
为“抽取的![]() 人中,三科成绩全及格的有
人中,三科成绩全及格的有![]() 人,三科成绩不全及格的有
人,三科成绩不全及格的有![]() 人”;事件
人”;事件![]() 为“抽取的
为“抽取的![]() 人中,三科成绩全及格的有
人中,三科成绩全及格的有![]() 人,三科成绩不全及格的有
人,三科成绩不全及格的有![]() 人”.有
人”.有![]() ,且
,且![]() 与
与![]() 互斥,根据①利用互斥事件的概率求解.
互斥,根据①利用互斥事件的概率求解.
(1)因为数学英语三个兴趣小组学生人数分别为10人10人15人,
所以语文数学英语三个兴趣小组的人数之比为![]() ,
,
因此,采用分层抽样方法从中抽取![]() 人,
人,
应从语文数学英语三个兴趣小组中分别抽取![]() 人
人![]() 人
人![]() 人.
人.
(2)①依题意,得随机变量![]() 的所有可能取值为
的所有可能取值为![]() .
.
所以,![]() .
.
因此,所求随机变量![]() 的分布列为
的分布列为

![]() .
.
②依题意,设事件![]() 为“抽取的
为“抽取的![]() 人中,三科成绩全及格的有
人中,三科成绩全及格的有![]() 人,三科成绩不全及格的有
人,三科成绩不全及格的有![]() 人”;事件
人”;事件![]() 为“抽取的
为“抽取的![]() 人中,三科成绩全及格的有
人中,三科成绩全及格的有![]() 人,三科成绩不全及格的有
人,三科成绩不全及格的有![]() 人”.
人”.
则有![]() ,且
,且![]() 与
与![]() 互斥.
互斥.
由①知,![]() ,
,
所以![]()
故事件![]() 发生的概率为
发生的概率为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】在单位圆O:x2+y2=1上任取一点P(x,y),圆O与x轴正向的交点是A,设将OA绕原点O旋转到OP所成的角为θ,记x,y关于θ的表达式分别为x=f(θ),y=g(θ),则下列说法正确的是( )
A.x=f(θ)是偶函数,y=g(θ)是奇函数
B.x=f(θ)在![]() 为增函数,y=g(θ)在
为增函数,y=g(θ)在![]() 为减函数
为减函数
C.f(θ)+g(θ)≥1对于![]() 恒成立
恒成立
D.函数t=2f(θ)+g(2θ)的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图一![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 折起,
折起,![]() 沿
沿![]() 折起,使得
折起,使得![]() ,
,![]() 重合于一点(如图二),设为
重合于一点(如图二),设为![]() .
.
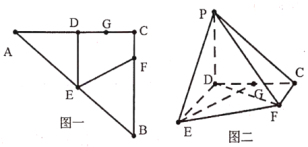
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
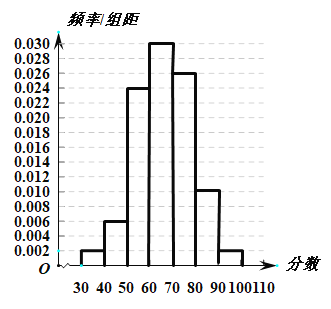
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AB=2CD=2PD=2,PC![]() ,且有PD⊥AD,AD⊥CD,AB∥CD.
,且有PD⊥AD,AD⊥CD,AB∥CD.

(1)证明:PD⊥平面ABCD;
(2)若四棱锥P﹣ABCD的体积为![]() ,求四棱锥P﹣ABCD的表面积.
,求四棱锥P﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,平面ABC是下底面.M是BB1上的点,AB=3,BC=4,AC=5,CC1=7,过三点A、M、C1作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com