练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某商场进行购物摸奖活动，规则是：在一个封闭的纸箱中装有标号分别为1，2，3，4，5，6的六个小球，每次摸奖需要同时取出两个球，每位顾客最多有两次摸奖机会，并规定：若第一次取出的两球号码连号，则中奖，摸奖结束；若第一次未中奖，则将这两个小球放回后进行第二次摸球，若与第一次取出的两个小球号码相同，则为中奖，按照这样的规则摸奖，中奖的概率为（　　）

    A.B.C.D.

    【答案】B

    【解析】

    可将中奖的情况分成第一次两球连号和第二次取出的小球与第一次取出的号码相同两种情况，分别计算两种情况的概率，根据和事件概率公式可求得结果.

    中奖的情况分为：第一次取出两球号码连号和第二次取出两个小球与第一次取出的号码相同两种情况

    第一次取出两球连号的概率为：

    第二次取出两个小球与第一次取出号码相同的概率为：

    中奖的概率为：

    本题正确选项：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在极坐标系中，曲线的极坐标方程为,以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，直线的参数方程为（t为参数).

    （1）写出曲线的参数方程和直线的普通方程；

    （2）已知点是曲线上一点，，求点到直线的最小距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线： 经过伸缩变换后得到曲线.以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）求出曲线、的参数方程；

    （Ⅱ）若、分别是曲线、上的动点，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表：

    温度x/C

    21

    23

    24

    27

    29

    32

    产卵数y/个

    6

    11

    20

    27

    57

    77

    经计算得： ， ， ， ，

    ，线性回归模型的残差平方和，e8.0605≈3167，其中xi, yi分别为观测数据中的温度和产卵数，i=1, 2, 3, 4, 5, 6.

    (Ⅰ)若用线性回归模型，求y关于x的回归方程=x+（精确到0.1）；

    (Ⅱ)若用非线性回归模型求得y关于x的回归方程为=0.06e0.2303x，且相关指数R2=0.9522.

    ( i )试与(Ⅰ)中的回归模型相比，用R2说明哪种模型的拟合效果更好.

    ( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数（结果取整数）.

    附：一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线=x+的斜率和截距的最小二乘估计为

    =；相关指数R2=．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中正确的个数①“，”的否定是“，”；②用相关指数可以刻画回归的拟合效果，值越小说明模型的拟合效果越好；③命题“若，则”的逆命题为真命题；④若的解集为，则.

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

    以最高气温位于各区间的频率估计最高气温位于该区间的概率.

    （1）求六月份这种酸奶一天的需求量（单位：瓶）的分布列；

    （2）设六月份一天销售这种酸奶的利润为（单位：元），当六月份这种酸奶一天的进货量（单位：瓶）为多少时，的数学期望达到最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，，

    ．

    （1）求证：；

    （2）当几何体的体积等于时，求四棱锥.的侧面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

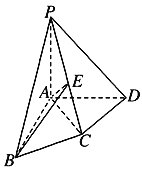
    【题目】如图，在四棱锥中，PA⊥平面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：

    (1)CD⊥AE；

    (2)PD⊥平面ABE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若，则称为的“不动点”，若，则称为的“稳定点”，函数的“不动点”和“稳定点”的集合分别记为和，即，那么，

    (1)求函数的“稳定点”;

    (2)若，且，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案