汽车在行使过程中,由于惯性作用,刹车制动后,还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.刹车距离是分析交通事故的一条重要因素.在一条限速为100km/h的高速公路上,甲车的刹车距离y(m)与刹车时的速度x(km/h)的关系可用函数模型y=ax2来描述.在这条高速公路上,甲车的速度为50km/h时,刹车距离为10m,则甲车的刹车距离为多少米时,交通部门可以判定此车超速?
解:∵刹车距离y(m)与刹车时的速度x(km/h)的关系为y=ax
2,
又∵甲车的速度为50km/h时,刹车距离为10m,
∴10=a•(50)
2,
∴a=
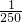
若判定此车超速,则
y>
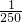
×(100)
2=40
答:甲车的刹车距离超过40米时,交通部门可以判定此车超速.
分析:由已知中甲车的刹车距离y(m)与刹车时的速度x(km/h)的关系可用函数模型y=ax
2来描述,根据甲车的速度为50km/h时,刹车距离为10m,我们可以求出参数a的值,进而求出甲车的速度为100km/h时的刹车距离,进而得到结论.
点评:本题考查的知识点是函数模型的选择与应用,其中根据条件,确定出y=ax
2中参数a的值,进而得到函数的解析式,是解答本题的关键.

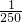
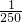 ×(100)2=40
×(100)2=40

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案