
分析 先画出满足条件的平面区域:(1)平移直线y=2x-z即可;(2)根据z=$\frac{y}{x}$表示直线的斜率结合图象求出即可;(3)根据两点的距离公式计算即可.
解答 解:平面区域M如如图所示: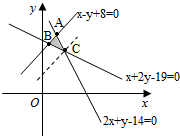
求得A(2,10),C(3,8),B(1,9);
(1)z=2x-y得:y=2x-z,
显然直线过B时z最小,过C时z最大,
∴Z最大值=-2,Z最小值=-8;
(2)由图象得:z=$\frac{y}{x}$得:
过OB的斜率最大,过OC的斜率最小,
∴Z最大值=$\frac{9}{1}$=9,Z最小值=$\frac{8}{3}$;
(3)z=x2+y2.
显然OA最大,
设原点O到直线BC的距离为d,
则:d=$\frac{19}{\sqrt{5}}$=$\frac{19\sqrt{5}}{5}$
∴Z最大值=4+100=104,Z最小值=d2=$\frac{361}{5}$.
点评 本题主要考查了用平面区域二元一次不等式组以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com