【题目】在甲、乙两个盒子中分别装有标号为
， 
， 
， 
的四个球，现从甲、乙两个盒子中各取出
个球，每个小球被取出的可能性相等.
（1）列出所有可能的结果；
（2）求取出的两个球上标号为相邻整数的概率；
（3）求取出的两个球上标号之和能被
整除的概率.
【答案】（1）见解析（2）
（3）
.
【解析】试题分析：（1）本题是一个古典概型，试验发生包含的事件是从两个盒子中分别取一个球，共有16种结果，满足条件的事件是所取两个小球上的数字为相邻整数，可以列举出所有结果，根据古典概型概率公式得到结果．
（2）满足条件的事件是所取两个小球上的数字之和能被3整除，列举出共有5种结果，得到概率；
（3）所取两个球上的数字和能被
整除的结果有共5种，即可得概率．
试题解析：
（1）设从甲、乙两个盒子中各取
个球，其数字分别为
， 
，用
表示抽取结果，则所有可能有
共16种.
（2）所取两个小球上的数字为相邻整数的结果有：
，共6种.
故所求概率
.
（3）所取两个球上的数字和能被
整除的结果有
共5种.故所求概率为
.
互动英语系列答案科目：高中数学 来源： 题型：
【题目】如图，抛物线
的焦点为
，抛物线上一定点
．
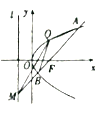
（1）求抛物线
的方程及准线
的方程；
（2）过焦点的直线（不经过
点）与抛物线交于
两点，与准线交于点
，记
的斜率分别为
，问是否存在常数
，使得
成立？若存在，求出的值；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着共享单车的成功运营，更多的共享产品逐步走入大家的世界，共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取
人对共享产品是否对日常生活有益进行了问卷调查，并对参与调查的
人中的性别以及意见进行了分类，得到的数据如下表所示：
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
（1）根据表中的数据，能否在犯错误的概率不超过
的前提下，认为对共享产品的态度与性别有关系？
（2）现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取
人，再从
人中随机抽取
人赠送超市购物券作为答谢，求恰有
人是女性的概率.
参与公式： 
临界值表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某营养学家建议：高中生每天的蛋白质摄入量控制在
（单位：克），脂肪的摄入量控制在
（单位：克），某学校食堂提供的伙食以食物
和食物
为主，1千克食物
含蛋白质60克，含脂肪9克，售价20元；1千克食物
含蛋白质30克，含脂肪27克，售价15元.
（1）如果某学生只吃食物
，判断他的伙食是否符合营养学家的建议，并说明理由；
（2）为了花费最低且符合营养学家的建议，学生需要每天同时食用食物
和食物
各多少千克？并求出最低需要花费的钱数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
（实数
为常数）
（1）当
时，证明
在
上单调递减；
（2）若
，且为偶函数，求实数
的值；
（3）小金同学在求解函数的对称中心时，发现函数是一个复合函数，设
，
，则
，显然
有对称中心，设为
，
有反函数
，则
的对称中心为
，请问小金的做法是否正确？如果正确，请给出证明，并直接写出当
时的对称中心；如果错误，请举出反例，并用正确的方法直接写出当时的对称中心.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，其中
、
为已知实常数，
.
下列所有正确命题的序号是____________．
①若
，则
对任意实数
恒成立；
②若
，则函数
为奇函数；
③若
，则函数为偶函数；
④当
时，若
，则
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于两个变量x和y进行回归分析，得到一组样本数据：
则下列说法不正确的是（ ）
A.由样本数据得到的回归直线
必经过样本点中心
B.残差平方和越小的模型，拟合的效果越好
C.用
来刻画回归效果，的值越小，说明模型的拟合效果越好
D.若变量y和x之间的相关系数
，则变量y和x之间具有线性相关关系
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
.
（1）若
，求实数
的取值范围；
（2）若存在
，使得
，求实数
的取值范围；
（3）若
对于
恒成立，试问是否存在实数，使得
成立？若存在，求出实数的值；若不存在，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
