
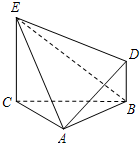
 已知△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,CE=CA=2BD=2.
已知△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,CE=CA=2BD=2.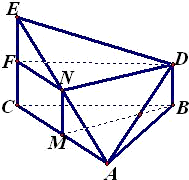
 EC.由BD=
EC.由BD= EC,且BD⊥平面ABC,
EC,且BD⊥平面ABC, ,由BD⊥平面ABC可得C到AB的距离即为C到面ABD的距离,
,由BD⊥平面ABC可得C到AB的距离即为C到面ABD的距离, ×
× ×DN•AE•h=
×DN•AE•h= ×S△ABD•d.
×S△ABD•d.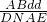 =
=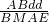 =
=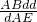 =
=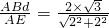 =
= .
.

科目:高中数学 来源:湖南省涟源市第一中2008届高三第二次月考文科数学试题 题型:044
如图,已知正三棱柱A1B1C1-ABC的底面边长为3a,侧棱长为![]() ,延长CB到D,使CB=BD.
,延长CB到D,使CB=BD.

(1)求证:直线C1B∥平面AB1D;
(2)求平面AB1D与平面ACB所成的二面角的大小;(结果用反三角表示)
(3)求点C1到平面AB1D的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角
形,AB⊥平面BCD,AB=BC=a,E为BC的中点,
F在棱AC上,且AF=3FC.
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,
使MN∥平面DEF?若存在,说明点N的位置;若不
存在,试说明理由.

查看答案和解析>>
科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学理) 题型:解答题
(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角
形,AB⊥平面BCD,AB=BC=a,E为BC的中点,
F在棱AC上,且AF=3FC.
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,
使MN∥平面DEF?若存在,说明点N的位置;若不
存在,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com