已知sinα+sinβ=1,cosα+cosβ=0,求cos(α+β)的值.
解:由已知sinα+sinβ=1①,
cosα+cosβ=0②,
①
2+②
2得:2+2cos(α-β)=1;
∴cos
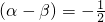
.
②
2-①
2得:cos2α+cos2β+2cos(α+β)=-1,
即2cos(α+β)〔cos(α-β)+1〕=-1.
∴cos(α+β)=-1.
分析:把已知的两个等式分别记作①和②,①
2+②
2后,利用同角三角函数间的基本关系及两角差的余弦函数公式化简后,得到cos(α-β)的值,然后再②
2-①
2后,利用两角和与差的正弦、余弦函数公式化简后,和差化积且提取cos(α+β),然后把cos(α-β)的值代入即可求出值.
点评:此题考查学生灵活运用两角和与差的余弦函数公式及同角三角函数间的基本关系化简求值,是一道基础题.此题的技巧性比较强,需要求出已知的两等式先平方差再相减,与和差公式联系计算.

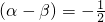 .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案