|
|
|
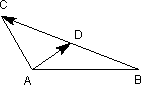
如下图,在△ABC中,AB=3,AC=2,D是边BC的中点,则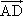 · ·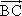 =________. =________.
|
|
|
答案:
解析:
|
-
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
椭圆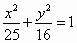 的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为 的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为
|
| [ ] |
A. |
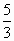
|
B. |
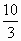
|
C. |
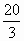
|
D. |
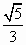
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设F1,F2是双曲线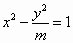 的两个焦点,过点F2作与x轴垂直的直线和双曲线的一个交点为A,满足| 的两个焦点,过点F2作与x轴垂直的直线和双曲线的一个交点为A,满足|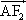 |=| |=|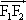 |,则双曲线的离心率为 |,则双曲线的离心率为
|
| [ ] |
A. |
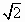
|
B. |
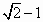
|
C. |
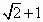
|
D. |
不确定,与m取值有关
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
“lgx,lgy,lgz成等差数列”是“y2=xz”成立的
|
| [ ] |
A. |
充分非必要条件;
|
B. |
必要非充分条件;
|
C. |
充要条件
|
D. |
既非充分也非必要条件
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在极坐标系中,点 关于直线l:ρcos 关于直线l:ρcos =1的对称点的一个极坐标为________. =1的对称点的一个极坐标为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,△ABC是直角三角形,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=2BC=4,EA=3,FC=1.
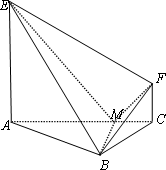
(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图所示的是一个算法的流程图,已知a1=3,输出的结果为7,则a2的值是
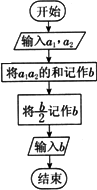
|
| [ ] |
A. |
9
|
B. |
10
|
C. |
11
|
D. |
12
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).


(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)若G为BC上的动点,求证:AE⊥PG.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
△ABC的三个内角A,B,C所对的边分别为a,b,c,向量 =(-1,1), =(-1,1), =(cosBcosC,sinBsinC- =(cosBcosC,sinBsinC- ),且 ),且 ⊥ ⊥ . .
(1)求A的大小;
(2)现在给出下列三个条件:①a=1;②2c-( +1)b=0;③B=45°,试从中选择两个条件以确定△ABC,求出所确定的△ABC的面积. +1)b=0;③B=45°,试从中选择两个条件以确定△ABC,求出所确定的△ABC的面积.
(注:只需要选择一种方案答题,如果用多种方案答题,则按第一方案给分).
|
|
|
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案