
【题目】在去年的足球甲![]() 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球.
A. 1个 B. 2个 C. 3个 D. 4个
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,直线
,直线![]() 与平面
与平面![]() 成
成![]() 角,
角, ![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() .
.

(Ⅰ)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)设![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的一个交点,且这两曲线在点
的一个交点,且这两曲线在点![]() 处的切线互相垂直,证明:存在唯一的实数
处的切线互相垂直,证明:存在唯一的实数![]() 满足题意,且
满足题意,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润. 
(1)将T表示为x的函数;
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈[100,110))则取x=105,且x=105的概率等于需求量落入[100,110)的频率,求T的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题,其中真命题的个数是( )
①若“![]() 或
或![]() ”是假命题,则“
”是假命题,则“![]() 且
且![]() ”是真命题;
”是真命题;
②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
③已知空间任意一点![]() 和不共线的三点
和不共线的三点![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
④直线![]() 与双曲线
与双曲线![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,则这样的直线有3条;
,则这样的直线有3条;
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,焦点为F,过点P(﹣1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若 ![]() +
+ ![]() =18,则k= .
=18,则k= .
查看答案和解析>>
科目:高中数学 来源: 题型:
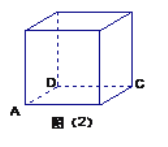
【题目】如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题。
(1)求证:MN∥平面PBD;
(2)求证:![]() 平面
平面![]() ;
;
(3)求PB和平面NMB所成的角的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com