练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题12分）在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1。（1）求证：平面ACD⊥平面ABC；（2）求二面角C-AB-D的大小。

    (Ⅰ)  见解析  (Ⅱ)   450


    解析:

    (1)证明：∵CD⊥AB，CD⊥BC，∴CD⊥平面ABC，

    又∵CD平面ACD，

    ∴平面ACD⊥平面ABC。

           （2）∵AB⊥BC，AB⊥CD，∴AB⊥平面BCD，

    ∴AB⊥BD，

                ∴∠CBD是二面角C-AB-D的平面角，

                ∵在Rt△BCD中，BC=CD，∴∠CBD=450。

                ∴二面角C-AB-D的大小为450。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011-2012学年湖北省八市高三三月联考理科数学 题型：解答题

    （本题满分12分）

    形状如图所示的三个游戏盘中（图（1）是正方形，M、N分别是所在边中点，图（2）是半径分别为2和4的两个同心圆，O为圆心，图（3）是正六边形,点P为其中心）各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．

    （I）一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？

    （II）用随机变量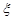表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量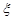的分布列及数学期望．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年山东省烟台市高三上学期模块检测数学文卷 题型：解答题

    本题满分12分）

    在一条笔直的工艺流水线上有三个工作台，将工艺流水线用如图所示的数轴表示，各工作台的坐标分别为，每个工作台上有若干名工人.现要在与之间修建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短.

    （1）若每个工作台上只有一名工人，试确定供应站的位置；

    （2）设三个工作台从左到右的人数依次为2，1，3，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值.

     

    查看答案和解析>>

    科目：高中数学 来源：2012届新课标高三下学期二轮复习理科数学综合验收试卷（3） 题型：解答题

    （本题满分12分）在如图所示的空间几何体中，平面平面ABC，

    AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在

    的平分线上。

     

     

    （1）求证：DE//平面ABC；

    （2）求二面角E—BC—A的余弦值；

     

    查看答案和解析>>

    科目：高中数学 来源：2010年黑龙江省高二上学期期中考试数学理卷 题型：解答题

    （本题12分）如图所示，已知圆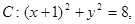定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足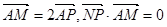，点N的轨迹为曲线E。      

    （1）求曲线E的方程； 

    （2）若过定点F（0，2）的直线交曲线E于G、H不同的两点，求此直线斜率的取值范围；

    （3）若点G在点F、H之间，且满足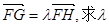的取值范围。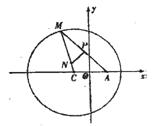

     

    查看答案和解析>>

    同步练习册答案