
【题目】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为 . 
【答案】41π
【解析】解:由三视图知该几何体是如图所示的三棱锥A﹣BCD,
将该三棱锥是放在棱长为4的正方体中,E是棱的中点,
所以三棱锥A﹣BCD和三棱柱DEF﹣ABC的外接球相同,
设外接球的球心为O、半径是R,△ABC外接圆的圆心是M,则OM=2,
在△ABC中,AB=AC=2 ![]() ,由余弦定理得,
,由余弦定理得,
cos∠CAB= ![]() =
= ![]() =
= ![]() ,
,
所以sin∠CAB= ![]() =
= ![]() ,
,
由正弦定理得,2CM= ![]() =5,则CM=
=5,则CM= ![]() ,
,
所以R=OC= ![]() =
= ![]()
则外接球的表面积S=4πR2=41π,
所以答案是:41π.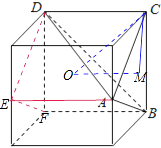
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识,掌握求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)当a=2时,求函数f(x)的最值;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点. 
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面APD⊥平面ABCD,且PA=PD=AD=2,在线段PC上是否存在点M,使二面角M﹣BQ﹣C的大小为60°.若存在,试确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如图所示.据此解答如下问题:
(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)根据茎叶图和频率分布直方图估计这次测试的平均分.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)+![]() x2-ax+1(a>1).
x2-ax+1(a>1).
(1)求函数y=f(x)在点(0,f(0))处的切线方程;
(2)当a>1时,求函数y=f(x)的单调区间和极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com