
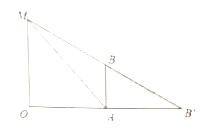
【题目】已知小明(如图中![]() 所示)身高
所示)身高![]() 米,路灯
米,路灯![]() 高
高![]() 米,
米, ![]() ,
, ![]() 均垂直于水平地面,分别与地面交于点
均垂直于水平地面,分别与地面交于点![]() ,
, ![]() .点光源从
.点光源从![]() 发出,小明在地上的影子记作
发出,小明在地上的影子记作![]() .
.
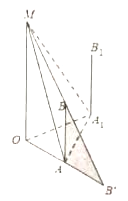
(1)小明沿着圆心为![]() ,半径为
,半径为![]() 米的圆周在地面上走一圈,求
米的圆周在地面上走一圈,求![]() 扫过的图形面积;
扫过的图形面积;
(2)若![]() 米,小明从
米,小明从![]() 出发,以
出发,以![]() 米/秒的速度沿线段
米/秒的速度沿线段![]() 走到
走到![]() ,
, ![]() ,且
,且![]() 米.
米. ![]() 秒时,小明在地面上的影子长度记为
秒时,小明在地面上的影子长度记为![]() (单位:米),求
(单位:米),求![]() 的表达式与最小值.
的表达式与最小值.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() ,
,![]() 两组.
两组.![]() 年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() ,
,![]() ,
,![]() ,
,![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
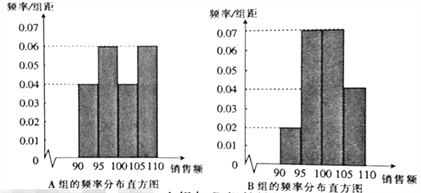
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() ,
,![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对本市小学生课业负担情况进行了调查,设平均每人每天做作业的时间为![]() 分钟,有1200名小学生参加了此项调查,调查所得到的数据用程序框图处理(如图),若输出的结果是840,若用样本频率估计概率,则平均每天做作业的时间在0~60分钟内的学生的概率是( )
分钟,有1200名小学生参加了此项调查,调查所得到的数据用程序框图处理(如图),若输出的结果是840,若用样本频率估计概率,则平均每天做作业的时间在0~60分钟内的学生的概率是( )

A. 0.32 B. 0.36 C. 0.7 D. 0.84
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com