
【题目】如图所示,抛物线![]() 的焦点为
的焦点为![]() .
.
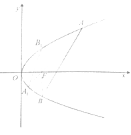
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的两条直线分别与抛物线
的两条直线分别与抛物线![]() 交于点
交于点![]() ,
,![]() 与
与![]() ,
,![]() (点
(点![]() ,
,![]() 在
在![]() 轴的上方).
轴的上方).
①若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
②设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,AC=1,AB=![]() ,BC=
,BC=![]() ,AA1=
,AA1=![]() .
.

(1)求证:A1B⊥B1C;
(2)求二面角A1—B1C—B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线y=﹣2x+1与圆O:x2+y2=r2(r>0)交于M,N两点,且MN=![]() .
.
(1)求M,N的坐标;
(2)求过O,M,N三点的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公园游园活动中,有这样一个游戏项目:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和2个黑球,这些球除颜色外完全相同.每次游戏都从这两个箱子里各随机地摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在每一次游戏中获奖的概率;
(2)在三次游戏中,记获奖次数为![]() ,求
,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个结论: ①数列可以看作是一个定义在正整数集(或它的有限子集{1,2,3……,n})上的函数;
②数列若用图象表示,从图象上看都是一群孤立的点;
③数列的项数是无限的;
④数列通项的表示式是唯一的.
其中正确的是( )
A.①②
B.①②③
C.②③
D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若0<a<b,且a+b=1,则下列各式中最大的是( )
A.﹣1
B.log2a+log2b+1
C.log2b
D.log2(a3+a2b+ab2+b3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1+x﹣ ![]() +…+
+…+ ![]() ,g(x)=1﹣x+
,g(x)=1﹣x+ ![]() ﹣…﹣
﹣…﹣ ![]() ,设函数F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
,设函数F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
A.9
B.10
C.11
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com