
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() 当点
当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
![]() 求曲线
求曲线![]() 的方程;
的方程;
![]() 已知直线
已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,设
,设![]() ,证明:直线
,证明:直线![]() 过定点,并求
过定点,并求![]() 面积的最大值.
面积的最大值.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,超过
收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司对近60天,每天揽件数量统计如下表:

(1)某人打算将![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过30元的概率;
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过30元的概率;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过150件,工资100元,目前前台有工作人员3人,那么,公司将前台工作人员裁员1人对提高公司利润是否更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴上,抛物线C上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
![]() Ⅰ
Ⅰ![]() 求抛物线C的标准方程;
求抛物线C的标准方程;
![]() Ⅱ
Ⅱ![]() 设点
设点![]() ,过点
,过点![]() 的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为
的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为![]() ,
,![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在![]() 内现将这100名学生的成绩按照
内现将这100名学生的成绩按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组后,得到的频率分布直方图如图所示,则下列说法正确的是
分组后,得到的频率分布直方图如图所示,则下列说法正确的是![]()
![]()
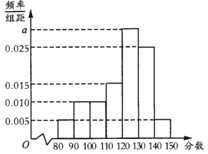
A. 频率分布直方图中a的值为![]()
B. 样本数据低于130分的频率为![]()
C. 总体的中位数![]() 保留1位小数
保留1位小数![]() 估计为
估计为![]() 分
分
D. 总体分布在![]() 的频数一定与总体分布在
的频数一定与总体分布在![]() 的频数相等
的频数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.
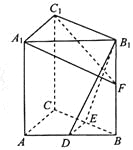
求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() ,
, ![]() 平面
平面![]() ,底面
,底面![]() 中,
中, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)问在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,请求出二面角
,若存在,请求出二面角![]() 的余弦值;若不存在,请说明理由.
的余弦值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com