
【题目】有一个墙角,两墙面所成二面角的大小为![]() 有一块长为
有一块长为![]() 米,宽为
米,宽为![]() 米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓
米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓![]() .
.
(1)当![]() 为多少米时,储物仓底面三角形
为多少米时,储物仓底面三角形![]() 面积最大?
面积最大?
(2)当![]() 为多少米时,储物仓的容积最大?
为多少米时,储物仓的容积最大?
(3)求储物仓侧面积的最大值.
【答案】(1)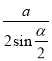 ;(2)
;(2)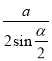 ;(3)
;(3)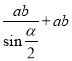
【解析】
(1)设![]() ,讨论
,讨论![]() 和
和![]() 两种情况,利用利用基本不等式得出底面三角形的面积的最大值;
两种情况,利用利用基本不等式得出底面三角形的面积的最大值;
(2)设![]() ,讨论
,讨论![]() 和
和![]() 两种情况,利用利用基本不等式得出三棱柱的体积的最大值;
两种情况,利用利用基本不等式得出三棱柱的体积的最大值;
(3)设![]() ,讨论
,讨论![]() 和
和![]() 两种情况,利用利用基本不等式得三棱柱的侧面积的最大值.
两种情况,利用利用基本不等式得三棱柱的侧面积的最大值.
解:如图所示:

(1)设![]() ,
,
①若![]() ,则
,则![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∴![]() ,
,
②若![]() ,同理可得
,同理可得![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
又![]() ,故当
,故当![]() ,
,![]() 时,储物仓底面三角形ABC的面积最大,
时,储物仓底面三角形ABC的面积最大,
此时,![]() 为等腰三角形,
为等腰三角形,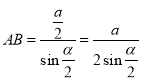 。
。
(2)设![]() ,
,
①若![]() ,由(1)①可知储物仓的容积
,由(1)①可知储物仓的容积![]() ,
,
②若![]() ,由(1)②可知储物仓的容积
,由(1)②可知储物仓的容积![]() ,
,
![]() 又
又 ![]() ,
,
![]() ,
,
由(1)可知当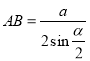 时,储物仓的容积最大.
时,储物仓的容积最大.
(3)设![]() ,
,
①若![]() ,则由余弦定理可得
,则由余弦定理可得![]() ,
,
![]() ,即
,即![]() ,
,
又![]() ,
,
解得:![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∴储物仓的侧面积为![]() ,
,
②若![]() ,同理可得储物仓的侧面积为
,同理可得储物仓的侧面积为![]() ,
,
综上,储物仓的侧面积的最大值为![]() 。
。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.在线性回归分析中,相关系数r的值越大,变量间的相关性越强
B.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在问归分析中,![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的全面积为2,记正四棱锥的高为h.
的全面积为2,记正四棱锥的高为h.

(1)用h表示底面边长,并求正四棱锥体积V的最大值;
(2)当V取最大值时,求异面直线AB和PD所成角的大小.![]() 结果用反三角函数值表示
结果用反三角函数值表示![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本市,随机对本市内![]() 岁的人群抽取了
岁的人群抽取了![]() 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |

(1)分别求出![]() 的值;
的值;
(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,部分
,部分![]() 与
与![]() 的对应关系如下表:
的对应关系如下表:
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | 2 | 0 | -1 | 0 | 2 |
(1)求![]() ;
;
(2)数列![]() 满足
满足![]() ,且对任意
,且对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上,求
的图像上,求![]() ;
;
(3)若![]() ,其中
,其中![]() ,求此函数的解析式,并求
,求此函数的解析式,并求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com