设函数f(x)=2x3+3ax2+3bx在x=1时取得极大值5
(1)求函数f(x)的解析式;
(2)对于任意的x∈[0,3],都有f(x)<m2-8m成立,求m的取值范围.
解:(1)∵f(x)=2x
3+3ax
2+3bx,
∴f'(x)=6x
2+6ax+3b…(1分)
∵函数f(x)=2x
3+3ax
2+3bx在x=1时取得极大值5,
∴
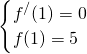
…(2分)
解得:a=-3,b=4,…(3分)
经检验:a=-3,b=4符合题意 …(4分)
∴f(x)=2x
3-9x
2+12x…(5分)
(2)对于任意的x∈[0,3],
都有f(x)<m
2-8m成立等价于2x
3-9x
2+12x<m
2-8m在[0,3]上恒成立,…(6分)
由f(x)=2x
3-9x
2+12x
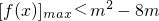
在[0,3]上恒成立,…(8分)
比较f(2),f(1),f(0),f(3)的大小,
得[f(x)]
max=9…(10分)
∴9<m
2-8m,…11 分
解得m>9或m<-1.…(12分)
分析:(1)由f(x)=2x
3+3ax
2+3bx在x=1时取得极大值5,知
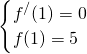
,解得a=-3,b=4,由此能求出函数f(x)的解析式.
(2)对于任意的x∈[0,3],都有f(x)<m
2-8m成立等价于2x
3-9x
2+12x<m
2-8m在[0,3]上恒成立.由f(x)=2x
3-9x
2+12x
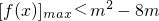
在[0,3]上恒成立,能求出m的取值范围.
点评:本题考查利用导数求闭区间上函数最值的应用,易错点是对于任意的x∈[0,3],都有f(x)<m
2-8m成立等价于2x
3-9x
2+12x<m
2-8m在[0,3]上恒成立.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

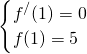 …(2分)
…(2分)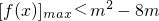 在[0,3]上恒成立,…(8分)
在[0,3]上恒成立,…(8分)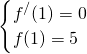 ,解得a=-3,b=4,由此能求出函数f(x)的解析式.
,解得a=-3,b=4,由此能求出函数f(x)的解析式.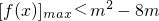 在[0,3]上恒成立,能求出m的取值范围.
在[0,3]上恒成立,能求出m的取值范围.
