练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知直线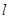与直线m是异面直线，直线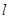在平面α内，在过直线m所作的所有平面中，下列结论正确的是    （   ）

    A．一定存在与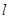平行的平面，也一定存在与α平行的平面
    B．一定存在与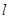平行的平面，也一定存在与α垂直的平面
    C．一定存在与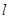垂直的平面，也一定存在与α平行的平面
    D．一定存在与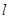垂直的平面，也一定存在与α垂直的平面

    B

    解析考点：空间中直线与平面之间的位置关系．
    专题：计算题．
    分析：A：当性质m与平面α斜交时，不存在与α平行的平面．B：根据空间中线面的位置关系可得：一定存在与l平行的平面，也一定存在与α垂直的平面．C：当直线l与m不垂直时，不存在与l垂直的平面．D：当直线l与m不垂直时，不存在与l垂直的平面．
    解答：解：A：根据空间中线面的位置关系可得：当性质m与平面α斜交时，不存在与α平行的平面．所以A错误．
    B：根据空间中线面的位置关系可得：一定存在与l平行的平面，也一定存在与α垂直的平面．所以B正确．
    C：由空间中线线的位置关系可得：当直线l与m不垂直时，不存在与l垂直的平面．所以C错误．
    D：由空间中线线的位置关系可得：当直线l与m不垂直时，不存在与l垂直的平面．所以D错误．
    故选B．
    点评：解决此类问题的关键是熟练掌握空间中线面与面面得位置关系，以及与其有关的判断定理与性质定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    17、已知 l，m，n是互不相同的直线，α，β是不同的平面，则下列四个命题：
    ①m?α，l∩α=A，点A∉m，则 l与 m 是异面直线；
    ②若l∥α，m∥β，α∥β，则l∥m；
    ③l、m是异面直线，l∥α，m∥α，且n⊥l，n⊥m，则n⊥α；
    ④若l?α，m?α，l∩m=A，l∥β，m∥β，则α∥β
    其中是真命题的是
    ①、③、④
    （请写出所有正确答案的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线m、n是异面直线，则过直线n且与直线m平行的平面（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题,则其中的真命题是

    A.若直线m、n都平行于平面α,则m、n一定不是相交直线

    B.已知平面α、β互相垂直,且直线m、n也互相垂直,若m⊥α,则n⊥β

    C.直线m、n在平面α内的射影分别是一个点和一条直线,且m⊥n,则nα或n∥α

    D.直线m、n是异面直线,若m∥α,则n必与α相交

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知以向量v=(1,)为方向向量的直线l过点(0,),抛物线C:y2=2px(p＞0)的顶点关于直线l的对称点在该抛物线的准线上.

    (1)求抛物线C的方程;

    (2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若+p2=0(O为原点,A、B异于原点),试求点N的轨迹方程.

    查看答案和解析>>

    同步练习册答案