练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某快递公司有两种发放薪水的方案：

    方案一：底薪1800元，设每月送快递单，提成(单位：元)为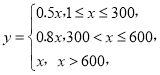

    方案二：底薪2000元，设每月送快递单，提成(单位：元)为

    以下该公司某职工小甲在2019年9月份(30天)送快递的数据，

    日送快递单数

    11

    13

    14

    15

    16

    18

    天数

    4

    5

    12

    3

    5

    1

    （1）从小甲日送快递单数大于15的六天中抽取两天，求这两天他送的快递单数恰好都为16单的概率.

    （2）请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案，并说明理由.

    【答案】（1）；（2）选择方案二，理由见解析.

    【解析】

    （1）列举法求出“从小甲日送快递单数大于15的六天中抽取两天”的所有抽取方式，求出“这两天他送的快递单数恰好都为16单”包含的抽取方式，根据古典概型的概率计算公式即求概率；

    （2）求出小甲的月送单量，代入两种方案求他的薪水，选择薪水较高的方案.

    （1）小甲日送快递单数为16的有5天，依次编号为，单数为18的有1天，编号为，从中抽取两天，

    共15种抽取方式.

    他送的快递单数恰好都为16单共有10种情况，

    所以这两天他送的快递单数恰好都为16单的概率为.

    （2）月送单量，

    方案一：薪水元，

    方案二：薪水元，

    因为，所以选择方案二.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某重点中学高三的一名学生在高考前对他在高三近一年中的所有数学考试(含模拟考试、月考、平时训练等各种类型的试卷)分数进行统计，以此来估计自己在高考中的大致分数.为此，随机抽取了若干份试卷作为样本，根据此样本数据作出如下频率分布统计表和频率分布直方图.

    分组

    频数

    频率

    20

    0.25

    50

    4

    0.05

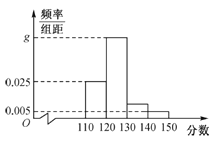
    （1）求表中的值和频率分布直方图中的值；

    （2）若同组中的每个数据用该组区间的中点值代替，试根据频率分布直方图求该学生高三年级数学考试分数的中位数和平均数，并对该学生自己在高考中的数学成绩进行预测.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，点为半圆上一动点，若过作椭圆的两切线分别交轴于、两点.

    （1）求证：；

    （2）当时，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，PC⊥平面ABCD，点M为PB中点，底面ABCD为梯形，AB∥CD，AD⊥CD，AD=CD=PC=AB.

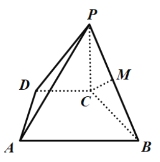
    （1）证明：CM∥平面PAD；

    （2）若四棱锥P-ABCD的体积为4，求点M到平面PAD的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】树立和践行“绿水青山就是金山银山，坚持人与自然和谐共生”的理念越来越深入人心，已形成了全民自觉参与，造福百姓的良性循环．据此，某网站退出了关于生态文明建设进展情况的调查，调查数据表明，环境治理和保护问题仍是百姓最为关心的热点，参与调查者中关注此问题的约占．现从参与关注生态文明建设的人群中随机选出200人，并将这200人按年龄分组：第1组，第2组，第3组，第4组，第5组，得到的频率分布直方图如图所示．

    （I）求出的值；

    （II）求出这200人年龄的样本平均数（同一组数据用该区间的中点值作代表）和中位数（精确到小数点后一位）；

    （III）现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人，再从这5人中随机抽取3人进行问卷调查，求第2组恰好抽到2人的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为正实数.

    讨论函数的单调性；

    若存在，使得不等式成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校设计了一个实验考察方案：考生从6道备选题中随机抽取3道题，按照题目要求独立完成全部实验操作，规定：至少正确完成其中的2道题便可通过．已知6道备选题中考生甲有4道能正确完成，2道题不能完成；考生乙每题正确完成的概率都是，且每题正确完成与否互不影响．

    （Ⅰ）求甲考生通过的概率

    （Ⅱ）求甲乙两考生正确完成题数的概率分布列和数学期望；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近几年市加大雾霾治理的投入，空气质量与前几年相比有了很大改善，并于年市入选中国空气优良城市.已知该市设有个监测站用于监测空气质量指数（），其中在轻度污染区、中度污染区、重度污染区分别设有、、个监测站，并以个监测站测得的的平均值为依据播报该市的空气质量.

    （1）若某日播报的为，已知轻度污染区平均值为，中度污染区平均值为，求重度污染区平均值；

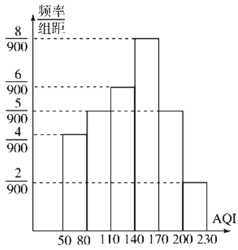
    （2）如图是年月份天的的频率分布直方图，月份仅有天在内.

    ①某校参照官方公布的，如果周日小于就组织学生参加户外活动，以统计数据中的频率为概率，求该校学生周日能参加户外活动的概率；

    ②环卫部门从月份不小于的数据中抽取两天的数据进行研究，求抽取的这两天中值在的天数的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】秉持“绿水青山就是金山银山”的生态文明发展理念，为推动新能源汽车产业迅速发展，有必要调查研究新能源汽车市场的生产与销售.下图是我国某地区年至年新能源汽车的销量（单位：万台）按季度（一年四个季度）统计制成的频率分布直方图.

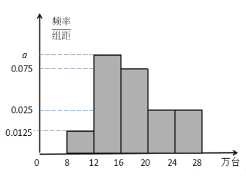
    （1）求直方图中的值，并估计销量的中位数；

    （2）请根据频率分布直方图估计新能源汽车平均每个季度的销售量（同一组数据用该组中间值代表），并以此预计年的销售量.

    查看答案和解析>>

    同步练习册答案