
【题目】在全球关注的抗击“新冠肺炎”中,某跨国科研中心的一个团队,研制了甲、乙两种治疗“新冠肺炎”新药,希望知道哪种新药更有效,为此进行动物试验,试验方案如下:
第一种:选取![]() 共10只患病白鼠,服用甲药后某项指标分别为:
共10只患病白鼠,服用甲药后某项指标分别为:![]() ;
;
第二种:选取![]() 共10只患病白鼠,服用乙药后某项指标分别为:
共10只患病白鼠,服用乙药后某项指标分别为:![]() ;
;
该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,记其中服药有效的只数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有![]() 变为正常白鼠,但正常白鼠仍有
变为正常白鼠,但正常白鼠仍有![]() 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用![]() 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为![]() .
.
(i)求![]() 并写出
并写出![]() 与
与![]() 的关系式;
的关系式;
(ii)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知过椭圆![]() 的四个顶点与坐标轴垂直的四条直线围成的矩形
的四个顶点与坐标轴垂直的四条直线围成的矩形![]() (
(![]() 是第一象限内的点)的面积为
是第一象限内的点)的面积为![]() ,且过椭圆
,且过椭圆![]() 的右焦点
的右焦点![]() 的倾斜角为
的倾斜角为![]() 的直线过点
的直线过点![]() .
.
(1)求椭圆![]() 的标准方程
的标准方程
(2)若射线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() .当它们的斜率之积为
.当它们的斜率之积为![]() 时,试问
时,试问![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 是等边三角形,
是等边三角形,![]() ,如图②,将
,如图②,将![]() 沿
沿![]() 折起使平面
折起使平面![]() 平面
平面![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
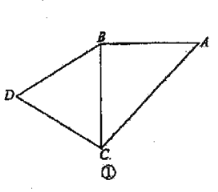
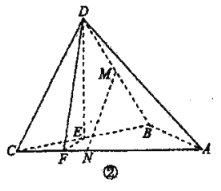
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下两个图表是2019年初的4个月我国四大城市的居民消费价格指数(上一年同月![]() )变化图表,则以下说法错误的是( )
)变化图表,则以下说法错误的是( )
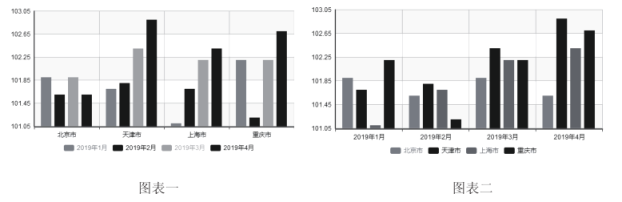
(注:图表一每个城市的条形图从左到右依次是1、2、3、4月份;图表二每个月份的条形图从左到右四个城市依次是北京、天津、上海、重庆)
A.3月份四个城市之间的居民消费价格指数与其它月份相比增长幅度较为平均
B.4月份仅有三个城市居民消费价格指数超过102
C.四个月的数据显示北京市的居民消费价格指数增长幅度波动较小
D.仅有天津市从年初开始居民消费价格指数的增长呈上升趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E为D1D的中点,AC与BD的交点为O.
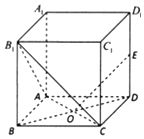
(1)求证:EO⊥平面AB1C;
(2)在由正方体的顶点确定的平面中,是否存在与平面AB1C平行的平面?证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() ,
, ![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | 18 | 30 |
非单车用户 | 38 | 32 | 70 |
合计 | 50 | 50 | 100 |
(1)从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关;
(2)将此样本的频率做为概率,从该市单车用户中随机抽取3人,记不小于40岁的单车用户的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: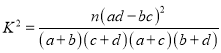 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com