
(1)求动点P的轨迹方程;
(2)直线3x-3my-2=0截动点P的轨迹所得弦长为2,求m的值;
(3)是否存在常数λ,使得∠PBC=λ∠PCB,若存在,求λ的值.若不存在,并请说明理由.
解:(1)由平面几何知识得:
|PA|-|PB|=|AN|-|BN|=![]()
∴动点P的轨迹是以A、B为焦点的双曲线(部分)
设它的方程为![]() ,则
,则
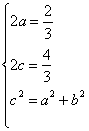 解得:
解得:
故所求的方程为
(2)设直线3x-3my-2=0与动点P的轨迹相交于点Q1(x1,y1)、Q2(x2,y2),
∵直线3x-3my-2=0恒过双曲线的焦点B
∴由双曲线定义知:
|Q1Q2|=e(x1+x2-![]() )=2(x1+x2-
)=2(x1+x2-![]() )=2
)=2
∴x1+x2=![]()
若m=0,则x1=x2=![]() ,此时x1+x2=
,此时x1+x2=![]() ,即|Q1Q2|=2合题意
,即|Q1Q2|=2合题意
若m≠0,由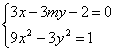
消去y得:9x2-3![]() ,化简得:
,化简得:
(27m2-9)x2+12x-3m2-4=0,x1+x2=![]()
解得m=0与m≠0矛盾. ∴m=0
(3)当x=![]() 时,|BP|=1,|BC|=1,此得∠PCB=45°,∠PBC=90°猜想λ=2
时,|BP|=1,|BC|=1,此得∠PCB=45°,∠PBC=90°猜想λ=2
当x≠![]() 时,设P(x,y)
时,设P(x,y)
则y2=-3(![]() ),且tan∠PCB=
),且tan∠PCB=![]()
∴tan2∠PCB=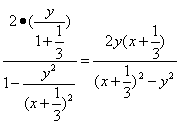

而tan∠PBC=-tan∠PBx=
∴tan2∠PBC=tan∠PBC
又∵0<∠PBC<π,0<2∠PBC<π
∠PBC=λ∠PBC.


科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:甘肃省嘉峪关市第一中学2011-2012学年高一上学期期末考试数学试题 题型:044
已知三角形三定点A(4,0),B(8,10),C(0,6);求
(1)AC边上的高所在的直线方程;
(2)过A点且平行与BC的直线方程
(3)求BC边的高
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
且|AN|-|BN|=![]() ,现分别过点A、B作动圆M的切线,两切线交于点P.
,现分别过点A、B作动圆M的切线,两切线交于点P.
(1)求动点P的轨迹方程;
(2)直线3x-3my-2=0截动点户的轨迹所得弦长为2,求m的值;
(3)求证:∠PAB=2∠PCB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com