
设![]() R
R![]()
(Ⅰ)求![]() 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,锐角A满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区期中理)(14分)
设![]() 是定义在区间D上的函数,若对任何实数
是定义在区间D上的函数,若对任何实数![]() 以及D中的任意两数
以及D中的任意两数![]() ,恒有
,恒有![]() ,则称
,则称![]() 为定义在D上的C函数.
为定义在D上的C函数.
(Ⅰ)试判断函数![]() ,
,![]() 是否为各自定义域上的C函数,并说明理由;
是否为各自定义域上的C函数,并说明理由;
(Ⅱ)已知![]() 是R上的C函数,m是给定的正整数,设
是R上的C函数,m是给定的正整数,设![]() ,且
,且![]() ,记
,记![]() . 对于满足条件的任意函数
. 对于满足条件的任意函数![]() ,试求
,试求![]() 的最大值;
的最大值;
(Ⅲ)若![]() 是定义域为R的函数,且最小正周期为
是定义域为R的函数,且最小正周期为![]() ,试证明
,试证明![]() 不是R上的C函数.
不是R上的C函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() 的定义域为R, 当x<0时,
的定义域为R, 当x<0时, ![]() >1, 且对于任意的实数
>1, 且对于任意的实数![]() , 有
, 有
![]() 成立. 又数列
成立. 又数列![]() 满足
满足![]() , 且
, 且![]()
(1)求证: ![]() 是R上的减函数;
是R上的减函数;
(2)求![]() 的值;
的值;
(3)若不等式![]() ≥k ?
≥k ?![]() 对一切
对一切![]() 均成立, 求
均成立, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省瓦房店市五校高二上学期竞赛数学理卷 题型:解答题
.(本小题满分12分)设函数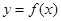 的定义域为R,当
的定义域为R,当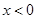 时,
时, ,且对任意实数
,且对任意实数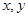 ,都有
,都有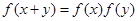 成立,数列
成立,数列 满足
满足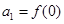 且
且
(1)求 的值;
的值;
(2)若不等式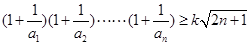 对一切
对一切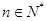 均成立,求
均成立,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com