
【题目】选修4—5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若存在实数![]() ,使得不等式
,使得不等式![]() 成立,求实
成立,求实![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据绝对值定义,将原不等式等价转化为三个不等式组,求它们的并集得原不等式的解集(2)不等式有解问题往往转化为对应函数最值问题:![]() ,由绝对值三角不等式得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,即转化为解不等式:
,由绝对值三角不等式得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,即转化为解不等式:![]() ,再利用绝对值定义求解得解集
,再利用绝对值定义求解得解集
试题解析:(1)当a=2时,f(x)=|x﹣3|﹣|x﹣2|,
当x≥3时,![]() ,即为
,即为![]() ,即
,即![]() 成立,则有x≥3;
成立,则有x≥3;
当x≤2时,![]() 即为
即为![]() ,即
,即![]() ,解得x∈;
,解得x∈;
当2<x<3时,![]() 即为
即为![]() ,解得,
,解得,![]() ,则有
,则有![]() .
.
则原不等式的解集为![]() 即为
即为![]() ;
;
(2)由绝对值不等式的性质可得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,
即有![]() 的最大值为|a﹣3|.
的最大值为|a﹣3|.
若存在实数x,使得不等式![]() 成立,则有
成立,则有![]()
即![]() 或
或![]() ,即有
,即有![]() ∈或
∈或![]() ≤
≤![]() .所以
.所以![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】在图所示的五面体中,面ABCD为直角梯形,![]() ,平面
,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() 是边长为2的正三角形.
是边长为2的正三角形.

![]() 证明:
证明:![]() 平面ACF;
平面ACF;
![]() 若点P在线段EF上,且二面角
若点P在线段EF上,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an} 和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(1)求{an}的通项公式;
(2)求和:b1+b3+b5+…+b2n-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求定义域,并判断函数f(x)的奇偶性;
(2)若f(1)+f(2)=0,证明函数f(x)在(0,+∞)上的单调性,并求函数f(x)在区间[1,4]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c,其中b,c∈R.
(1)当f(x)的图象关于直线x=1对称时,b=______;
(2)如果f(x)在区间[-1,1]不是单调函数,证明:对任意x∈R,都有f(x)>c-1;
(3)如果f(x)在区间(0,1)上有两个不同的零点.求c2+(1+b)c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中文“函数”(function)一词,最早由近代数学家李善兰翻译的之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化下列选项中两个函数相等的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
: ![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点.
两点.

(1)若直线![]() ,
, ![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过定点;
过定点;
(2)若线段![]() 的中点
的中点![]() 在曲线
在曲线![]() :
: ![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品近一个月内(30天)预计日销量![]() (件)与时间t(天)的关系如图1所示,单价
(件)与时间t(天)的关系如图1所示,单价![]() (万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
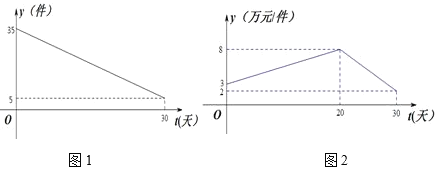
(1)试写出![]() 与
与![]() 的解析式;
的解析式;
(2)求此商品日销售额的最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com