
分析 (1)利用绝对值的意义,分类讨论解不等式f(x)≤1;
(2)对于任意x∈R都有a(x+3)≥f(x)成立,数形结合求实数a的取值范围.
解答 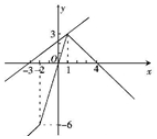 解:(1)x≤-2时,x-4≤1,得x≤5,∴x≤-2;
解:(1)x≤-2时,x-4≤1,得x≤5,∴x≤-2;
-2<x<1时,3x≤1,得x≤$\frac{1}{3}$,∴-2<x≤$\frac{1}{3}$;
x≥1时,-x+4≤1,得x≥3,∴x≥3,
综上所述,不等式的解集是{x|x$≤\frac{1}{3}$或x≥3};
(2)函数f(x)的图象如图所示,
∵y=a(x+3)过(-3,0),且在函数y=f(x)的图象的上方,过(-3,0),(1,3)的斜率为$\frac{3}{4}$,
∴$\frac{3}{4}$≤a≤1.
点评 本题考查绝对值不等式的解法,考查恒成立问题,考查数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
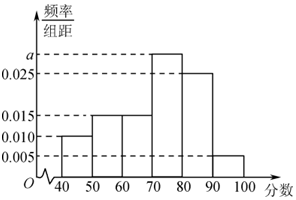 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…[90,100),后得到频率分布直方图(如图所示)
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…[90,100),后得到频率分布直方图(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一种 | B. | 第二种 | C. | 两种一样 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
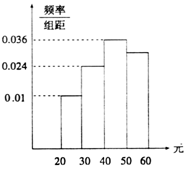 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )| A. | 10 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com