
【题目】如图,M是矩形ABCD的边CD上的一点,AC与BM交于点N,BN=![]() BM.
BM.

(1)求证:M是CD的中点;
(2)若AB=2,BC=1,H是BM上异于点B的一动点,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)0
【解析】
(1) 设![]() =m
=m![]() =n
=n![]() ,再根据向量的线性运算化简
,再根据向量的线性运算化简![]() =
=![]() ,再求出
,再求出![]() =(1-n)
=(1-n)![]() +n
+n![]() ,解方程组
,解方程组 所以
所以![]() =m
=m![]() ,即M是CD的中点.(2)先利用向量的数量积和向量的线性运算求得
,即M是CD的中点.(2)先利用向量的数量积和向量的线性运算求得![]() ==-
==-![]() ,再利用二次函数求出函数的最小值.
,再利用二次函数求出函数的最小值.
(1)设![]() =m
=m![]() =n
=n![]() ,
,
由题意知![]() )
)
=![]() +m
+m![]() )=
)=![]() ,
,
又![]() +n
+n![]() +n(
+n(![]() )
)
=(1-n)![]() +n
+n![]() ,
,
∴
∴![]() =m
=m![]() ,即M是CD的中点.
,即M是CD的中点.
(2)∵AB=2,BC=1,M是CD的中点,
∴MB=![]() ,∠ABM=45°,
,∠ABM=45°,
∴![]() =(
=(![]() )·
)·![]() =-(
=-(![]() )·
)·![]() =-
=-![]() -|
-|![]() |2
|2
=-|![]() ||
||![]() |cos(180°-∠ABH)-|
|cos(180°-∠ABH)-|![]() |2
|2
=|![]() ||
||![]() |cos 45°-|
|cos 45°-|![]() |2
|2
=![]() |-|
|-|![]() |2=-
|2=-![]() ,
,
又0<|![]() |≤
|≤![]() ,∴当|
,∴当|![]() |=
|=![]() ,即H与M重合时,
,即H与M重合时,![]() 取得最小值,且最小值为0.
取得最小值,且最小值为0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABNCD,EF∥AB,AB=2,BC=EF=1,AE= ![]() ,∠BAD=60°,G为BC的中点.
,∠BAD=60°,G为BC的中点. 
(1)求证:FG∥平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx,则“b<0”是“f(f(x))的最小值与f(x)的最小值相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .圆
.圆![]() :
: ![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,圆
,圆![]() 与
与![]() 轴相交于两点
轴相交于两点![]() (点
(点![]() 在点
在点![]() 的右侧).过点
的右侧).过点![]() 任作一条倾斜角不为0的直线与圆
任作一条倾斜角不为0的直线与圆![]() 相交于
相交于![]() 两点.问:是否存在实数
两点.问:是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a3 , a5 , a15成等比数列,若a1=3,Sn为数列an的前n项和,则anSn的最小值为( )
A.0
B.﹣3
C.﹣20
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 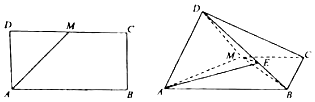
(1)求证:AD⊥BM;
(2)若 ![]() =2
=2 ![]() ,求二面角E﹣AM﹣D的正弦值.
,求二面角E﹣AM﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数既是奇函数,又在[﹣1,1]上单调递增是( )
A.f(x)=|sinx|
B.f(x)=ln ![]()
C.f(x)= ![]() (ex﹣e﹣x)
(ex﹣e﹣x)
D.f(x)=ln( ![]() ﹣x)
﹣x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com